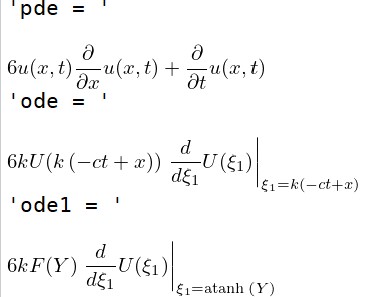python (SymPy) giving different result to Maple-CodePudding

I am trying to convert some Maple code to python using SymPy. The following is the Maple code I am trying to convert:

The following is my attempt at python code to do the same, but this is as far as I got.

from sympy import *
c, k, x, t, tau, Y, xi = symbols('c k x t tau Y xi')

u = Function('u')
F = Function('F') 
xi = k*(x-c*t)

U = Function('U')
pde = diff(u(x,t), t)   6*u(x,t)*diff(u(x,t), x) 
ode = simplify(pde.xreplace({t:tau,u(x,t):U(xi)}))
ode1 = simplify(ode.xreplace({xi:atanh(Y), U(xi):F(Y)}))

display('pde = ', pde)
display('ode = ', ode)
display('ode1 = ', ode1)

The output generated by python is:

The ode1 output from python should be the same (or similar) to the Maple output "F1".

Any help appreciated.

CodePudding user response：

This line: pde = diff(u(x,t), t) 6*u(x,t)*diff(u(x,t), x) reads pde = diff(u(x,t), x) 6*u(x,t)*diff(u(x,t), x) in your maple example, that might be the culprit.

CodePudding user response：

Notice first that your Python code defines the Python variable xi in two different ways. You need to distinguish between xi the symbol and the expression k*(x - c*t) so let's call the expression xi_e instead:

In [30]: from sympy import *
    ...: c, k, x, t, tau, Y, xi = symbols('c k x t tau Y xi')
    ...: 
    ...: u = Function('u')
    ...: F = Function('F')
    ...: xi_e = k*(x-c*t)
    ...: 
    ...: U = Function('U')
    ...: pde = diff(u(x,t), t)   6*u(x,t)*diff(u(x,t), x)

In [31]: pde
Out[31]: 
          ∂             ∂          
6⋅u(x, t)⋅──(u(x, t))   ──(u(x, t))
          ∂x            ∂t

Now we need to use xi and xi_e in different ways here and we have to be careful about the order of substitutions. I'll show each step so you can see what's happening:

In [35]: pde.xreplace({u(x,t):U(xi_e)})
Out[35]: 
                  ∂                     ∂                  
6⋅U(k⋅(-c⋅t   x))⋅──(U(k⋅(-c⋅t   x)))   ──(U(k⋅(-c⋅t   x)))
                  ∂x                    ∂t                 

In [36]: pde.xreplace({u(x,t):U(xi_e)}).xreplace({t: tau})
Out[36]: 
                  ∂                     ∂                  
6⋅U(k⋅(-c⋅τ   x))⋅──(U(k⋅(-c⋅τ   x)))   ──(U(k⋅(-c⋅τ   x)))
                  ∂x                    ∂τ                 

In [37]: pde.xreplace({u(x,t):U(xi_e)}).xreplace({t: tau}).doit()
Out[37]: 
      ⎛ d        ⎞│                                      ⎛ d        ⎞│               
- c⋅k⋅⎜───(U(ξ₁))⎟│                  6⋅k⋅U(k⋅(-c⋅τ   x))⋅⎜───(U(ξ₁))⎟│               
      ⎝dξ₁       ⎠│ξ₁=k⋅(-c⋅τ   x)                       ⎝dξ₁       ⎠│ξ₁=k⋅(-c⋅τ   x)

In [40]: pde.xreplace({u(x,t):U(xi_e)}).xreplace({t: tau}).doit().xreplace({x: xi/k   c*tau})
Out[40]: 
      ⎛ d        ⎞│                ⎛ d        ⎞│    
- c⋅k⋅⎜───(U(ξ₁))⎟│       6⋅k⋅U(ξ)⋅⎜───(U(ξ₁))⎟│    
      ⎝dξ₁       ⎠│ξ₁=ξ            ⎝dξ₁       ⎠│ξ₁=ξ

In [41]: pde.xreplace({u(x,t):U(xi_e)}).xreplace({t: tau}).doit().xreplace({x: xi/k   c*tau}).doit()
Out[41]: 
      d                   d       
- c⋅k⋅──(U(ξ))   6⋅k⋅U(ξ)⋅──(U(ξ))
      dξ                  dξ

That's your ode1 shown in your Maple code (or ode in the Python code):

In [42]: ode = pde.xreplace({u(x,t):U(xi_e)}).xreplace({t: tau}).doit().xreplace({x: xi/k   c*tau}).doit()

In [43]: ode
Out[43]: 
      d                   d       
- c⋅k⋅──(U(ξ))   6⋅k⋅U(ξ)⋅──(U(ξ))
      dξ                  dξ

Next you want to replace xi with atanh(Y) and U(xi) with F(Y). In Maple you are using dchange for this but SymPy does not have an equivalent for dchange to change the variable being differentiated wrt. There is an open issue to add something like dchange: https://github.com/sympy/sympy/issues/17590

In that issue you can see some example code that can do this. It just involves a bit of fiddling with intermediate variables. I'll show all of the steps so you can see what's happening:

In [44]: xi_f = Function('xi')

In [45]: xi_s = atanh(Y)

In [46]: diff_xi = lambda e, n: Derivative(e, Y) / Derivative(xi_f(Y), Y)

In [47]: changex = lambda e: e.replace(Derivative, lambda e, vs: diff_xi(e, vs[1]))

In [50]: eqf = ode.subs(xi, xi_f(Y))

In [51]: eqf
Out[51]: 
        d                            d           
- c⋅k⋅─────(U(ξ(Y)))   6⋅k⋅U(ξ(Y))⋅─────(U(ξ(Y)))
      dξ(Y)                        dξ(Y)  

In [61]: changex(eqf)
Out[61]: 
      d                         d          
  c⋅k⋅──(U(ξ(Y)))   6⋅k⋅U(ξ(Y))⋅──(U(ξ(Y)))
      dY                        dY         
- ───────────────   ───────────────────────
      d                     d              
      ──(ξ(Y))              ──(ξ(Y))       
      dY                    dY             

In [62]: changex(eqf).xreplace({U(xi_f(Y)): F(Y)})
Out[62]: 
      d                   d       
  c⋅k⋅──(F(Y))   6⋅k⋅F(Y)⋅──(F(Y))
      dY                  dY      
- ────────────   ─────────────────
    d                 d           
    ──(ξ(Y))          ──(ξ(Y))    
    dY                dY          

In [63]: changex(eqf).xreplace({U(xi_f(Y)): F(Y)}).xreplace({xi_f(Y): xi_s})
Out[63]: 
      d                   d       
  c⋅k⋅──(F(Y))   6⋅k⋅F(Y)⋅──(F(Y))
      dY                  dY      
- ────────────   ─────────────────
  d                 d             
  ──(atanh(Y))      ──(atanh(Y))  
  dY                dY            

In [64]: changex(eqf).xreplace({U(xi_f(Y)): F(Y)}).xreplace({xi_f(Y): xi_s}).doit()
Out[64]: 
      ⎛     2⎞ d              ⎛     2⎞      d       
- c⋅k⋅⎝1 - Y ⎠⋅──(F(Y))   6⋅k⋅⎝1 - Y ⎠⋅F(Y)⋅──(F(Y))
               dY                           dY

That matches your final ode1.