How to modify a 3d array using numpy block without for loop?-CodePudding

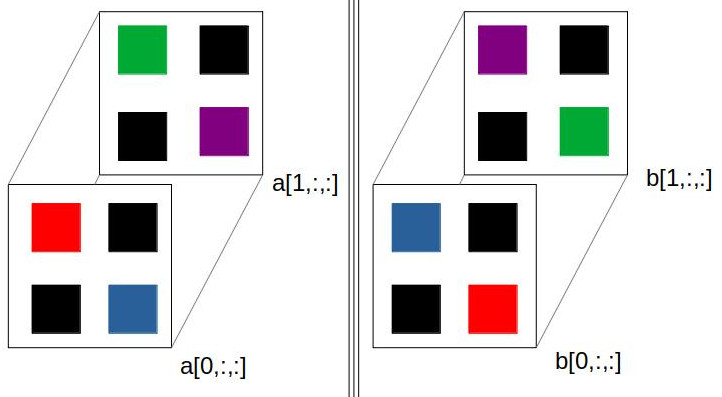
I want to modify block elements of 3d array without for loop. Without loop because it is the bottleneck of my code.

To illustrate what I want, I draw a figure:

The code with for loop:

import numpy as np

# Create 3d array with 2x4x4 elements
a = np.arange(2*4*4).reshape(2,4,4)
b = np.zeros(np.shape(a))

# Change Block Elements

for it1 in range(2):
    b[it1]= np.block([[a[it1,0:2,0:2], a[it1,2:4,0:2]],[a[it1,0:2,2:4], a[it1,2:4,2:4]]] )

CodePudding user response：

Will it make it faster?

import numpy as np
a = np.arange(2*4*4).reshape(2,4,4)
b = a.copy()
b[:,0:2,2:4], b[:,2:4,0:2] = b[:,2:4,0:2].copy(), b[:,0:2,2:4].copy()

Comparison with np.block() alternative from another answer.

Option 1:

%timeit b = a.copy(); b[:,0:2,2:4], b[:,2:4,0:2] = b[:,2:4,0:2].copy(), b[:,0:2,2:4].copy()

Output:

5.44 µs ± 134 ns per loop (mean ± std. dev. of 7 runs, 100,000 loops each)

Option 2

%timeit b = np.block([[a[:,0:2,0:2], a[:,2:4,0:2]],[a[:,0:2,2:4], a[:,2:4,2:4]]])

Output:

30.6 µs ± 1.75 µs per loop (mean ± std. dev. of 7 runs, 10,000 loops each)

CodePudding user response：

You can directly replace the it1 by a slice of the whole dimension:

b = np.block([[a[:,0:2,0:2], a[:,2:4,0:2]],[a[:,0:2,2:4], a[:,2:4,2:4]]])

CodePudding user response：

First let's see if there's a way to do what you want for a 2D array using only indexing, reshape, and transpose operations. If there is, then there's a good chance that you can extend it to a larger number of dimensions.

x = np.arange(2 * 3 * 2 * 5).reshape(2 * 3, 2 * 5)

Clearly you can reshape this into an array that has the blocks along a separate dimension:

x.reshape(2, 3, 2, 5)

Then you can transpose the resulting blocks:

x.reshape(2, 3, 2, 5).transpose(2, 1, 0, 3)

So far, none of the data has been copied. To make the copy happen, reshape back into the original shape:

x.reshape(2, 3, 2, 5).transpose(2, 1, 0, 3).reshape(2 * 3, 2 * 5)

Adding additional leading dimensions is as simple as increasing the number of the dimensions you want to swap:

b = a.reshape(a.shape[0], 2, a.shape[1] // 2, 2, a.shape[2] // 2).transpose(0, 3, 2, 1, 4).reshape(a.shape)

Here is a quick benchmark of the other implementations with your original array:

a = np.arange(2*4*4).reshape(2,4,4)

%%timeit
b = np.zeros(np.shape(a))
for it1 in range(2):
    b[it1] = np.block([[a[it1, 0:2, 0:2], a[it1, 2:4, 0:2]], [a[it1, 0:2, 2:4], a[it1, 2:4, 2:4]]])
    
27.7 µs ± 107 ns per loop (mean ± std. dev. of 7 runs, 10000 loops each)

%%timeit
b = a.copy()
b[:,0:2,2:4], b[:,2:4,0:2] = b[:,2:4,0:2].copy(), b[:,0:2,2:4].copy()

2.22 µs ± 3.89 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

%timeit b = np.block([[a[:,0:2,0:2], a[:,2:4,0:2]],[a[:,0:2,2:4], a[:,2:4,2:4]]])

13.6 µs ± 217 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

%timeit b = a.reshape(a.shape[0], 2, a.shape[1] // 2, 2, a.shape[2] // 2).transpose(0, 3, 2, 1, 4).reshape(a.shape)

1.27 µs ± 14.7 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)

For small arrays, the differences can sometimes be attributed to overhead. Here is a more meaningful comparison with arrays of size 10x1000x1000, split into 10 500x500 blocks:

a = np.arange(10*1000*1000).reshape(10, 1000, 1000)

%%timeit
b = np.zeros(np.shape(a))
for it1 in range(10):
    b[it1]= np.block([[a[it1,0:500,0:500], a[it1,500:1000,0:500]],[a[it1,0:500,500:1000], a[it1,500:1000,500:1000]]])

58 ms ± 904 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%%timeit
b = a.copy()
b[:,0:500,500:1000], b[:,500:1000,0:500] = b[:,500:1000,0:500].copy(), b[:,0:500,500:1000].copy()

41.2 ms ± 688 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit b = np.block([[a[:,0:500,0:500], a[:,500:1000,0:500]],[a[:,0:500,500:1000], a[:,500:1000,500:1000]]])

27.5 ms ± 569 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

%timeit b = a.reshape(a.shape[0], 2, a.shape[1] // 2, 2, a.shape[2] // 2).transpose(0, 3, 2, 1, 4).reshape(a.shape)

20 ms ± 161 µs per loop (mean ± std. dev. of 7 runs, 10 loops each)

So it seems that using numpy's own reshaping and transposition mechanism is fastest on my computer. Also, notice that the overhead of np.block becomes less important than copying the temporary arrays as size gets bigger, so the other two implementations change places.