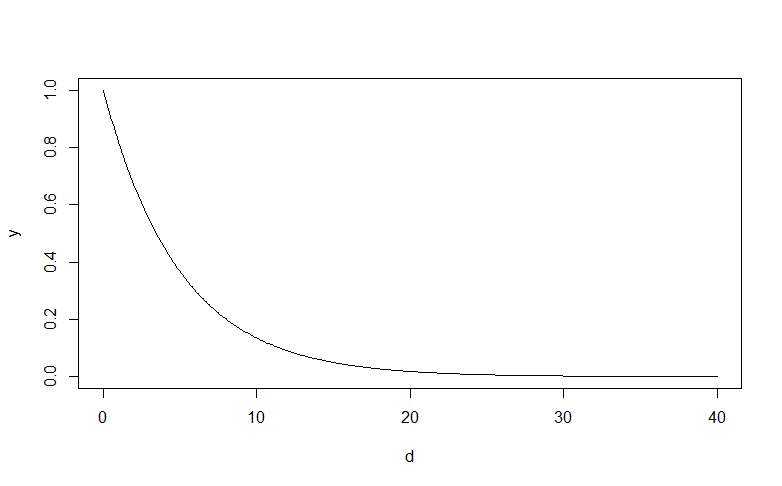set asymptote for negative exponential function-CodePudding

I have a function that produces a negative exponential curve.

Currently, as d increases y asymptotes towards 0.

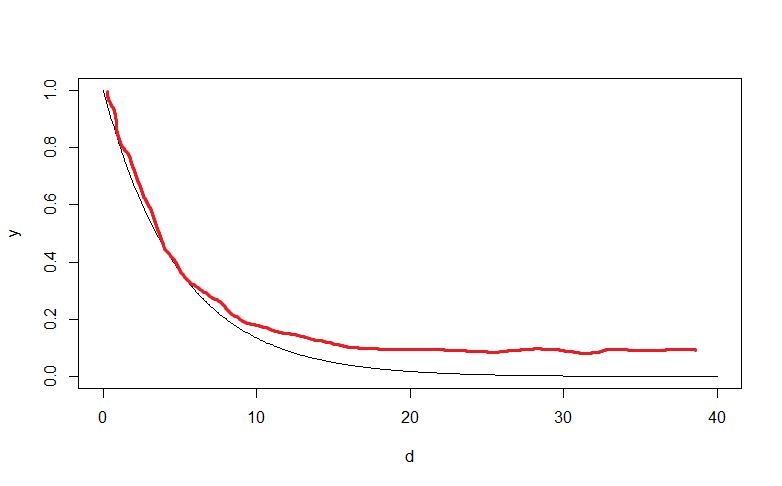
I would like to adjust the equation so that y asymptotes at some other value e.g. 0.1., the only other rule I need to keep to is that y cannot be greater than 1.

d will always be => 0

fun_expo <- function(d, z) {
  exp(-d/z)
}

d <- seq(0, 40, by = 0.1)
y <- fun_expo(d, z = 5)

plot(d, y,
     type = "l",
     xlab = "d",
     ylab = "y")

I started off by just adding a constant of 0.1 to my equation e.g.

fun_expo <- function(d, z) {
      exp(-d/z)   0.1
    }

But this results in y > 1 if d is lo, which I don't want to be possible.

I am hoping for an equation that would produce something like the following (the red line is what I want).

Any advice would be greatly appreciated.

CodePudding user response：

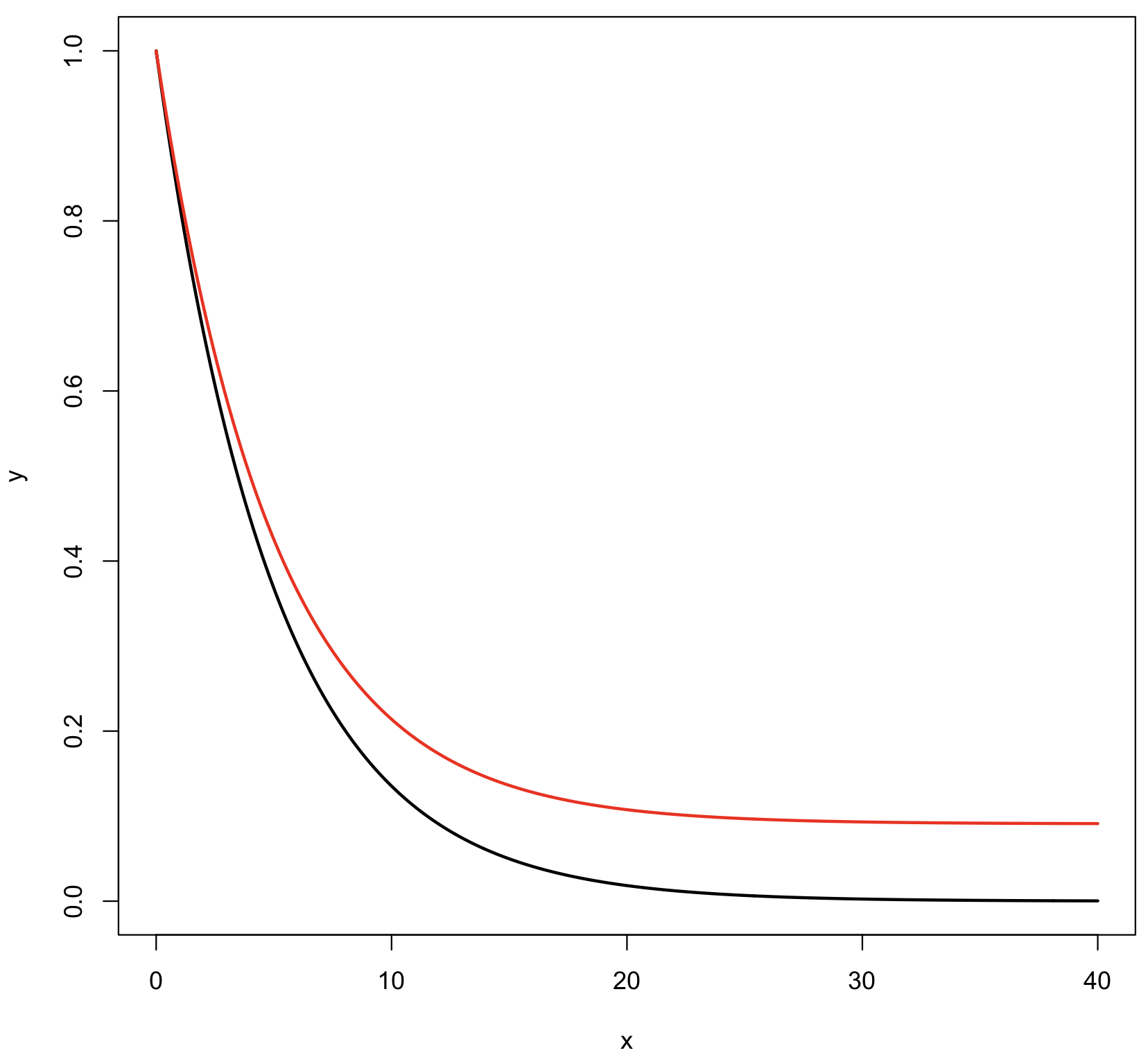
You just need to adjust the range on the vertical axis:

d <- seq(0, 40, by = 0.1)
y <- fun_expo(d, z = 5)
plot(x, y, type="l", lwd=2)
lines(x, (y   .1)/1.1, col="red", lwd=2)

CodePudding user response：

I figured it out. I'll leave an answer here in case it is helpful for others.

I just needed to add a multiplication scalar to the equation, now it works as intended. In the below example, z controls the "shape" of the line and b0 is the lower limit, where the line will asymptote.

fun_expo <- function(d, z, b0) {
  (1-b0) * exp(-d * z)   b0
}

d <- seq(0, 20, by = 1)
y <- fun_expo (d, z = 0.8, b0 = 0.1)

plot(d, y,
     type = "l",
     xlab = "d",
     ylab = "y")