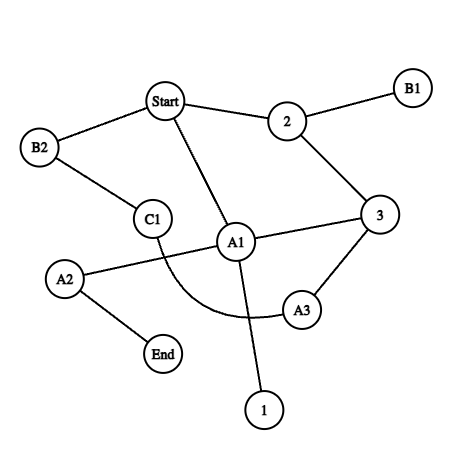
I can't figure out how to proceed with the following problem. Say I have an unoriented graph with an end node and a start node, I need to find the shortest path between these two nodes, but the path must include all mustpass node types.

There can be up to 10 of these types. This means that I should visit at least one node of each type (marked with a letter in the image) and then go to the end. Once I visit one of the nodes of type B, I may, but need not, visit other nodes of type B. The nodes that are marked with a number simply form a path and do not need to be visited.

This question is very similar to this. There it was suggested to find the shortest path between all the crucial nodes and then use the DFS algorithm. Can I apply the same algorithm to this problem?

CodePudding user response：

Let N be the number of vertices and M be the number of edges.

Break down the solution into two phases.

Phase 1: Compute the distance between each pair of edges. If the edges are not weighted, this can be easily done by starting a BFS from each node, spending a total of O(N(N M)) time. If the edges are weighted, you can you the Dijkstra's algorithm on each node, spending a total of O(N(NlogN M)) time.

After this phase, we have computed dist(x,y) for any pair of nodes x,y.

Phase 2: Now that we can query the distance between any pair of nodes in O(1) using the precomputed values in phase 1, it is time to put everything together. I can propose two possibilities here

Possibility 1: Us a similar approach as in the thread you linked. There are 1! factorial orders in which you could visit each node. Let's say we have fixed one possible order [s,t1,t2,...,t10,e] (where s and e are the start / end nodes, and ti represents a type) and we are trying to find out what would be the most optimal way to visit the nodes from start to finish in that order. Since each type can have multiple nodes belonging to it, it is not as simple as querying distances for every consecutive types t_i and t_{i 1}. What we should do instead if, for every node x, compute the fastest way to reach the end node from node x while respecting the order of types [s,t1,...,t10,e]. So if x is of type t_i, then we are looking for a way to reach e from x while visiting nodes of types t_{i 1}, t_{i 2}, ... t_{10} in that order. Call this value dp[x] (where dp stands for dynamic-programming). We are looking to find dp[s]. How do we compute dp[x] for a given node x? Simple - iterate through all nodes y of type t_{i 1} and consider d(x,y) dp[y]. Then we have dp[x] = min{dist(x,y) dp[y] for all y of type t_{i 1}}. Note that we need to compute dp[x] starting from the nodes of type t_10 all the way back to the nodes of type t_1. The complexity here is O(10! * N^2)

Possibility 2: There is actually a much faster way to find the answer and reduce the complexity to O(2^10 * N^3) (which can give massive gains for large N, and especially for larger number of node types (like 20 instead of 10)). To accomplish this we do the following. For each subset S of the set of types {1,2,...10}, and for each pair of nodes x, y with types in S define dp[S][x][y], which represents the fastest way to traverse the graph starting from node x, ending in node y and visiting all at least one node for every type in S. Note that we don't care about the actual order. To compute dp[S][x][y] for a given (S,x,y), all we need to do is go over all the possibilities for the second type to visit (node z with type t3). then we update dp[S][x][y] according dist(x,z) dp[S-t1][z][y] (where t1 is the type of the node x). The number of all the possible subsets along with start and end nodes is 2^10 * N^2. To compute each dp, we consider N possibilities for the second node to visit. So overall we get O(2^10 * N^3)

Note: in all of my analysis above, you can replace the value 10, with a more general K, representing the number of different types possible.