i am trying to solve the equation of motion for a particle with mass m attached to a spring with a spring constant k. Both are set to 1 however. The algorithm looks like this:

My (attempted) solution, written in c , looks like this:

#include <iostream>
#include <iomanip>
#include <math.h>
#include <stdlib.h>
#include <fstream>

// Initialise file to write series of values in
std::ofstream output("Eulermethod.txt");

// Define Euler algorithm
void euler(double x_0, double v_0, double delta, double t_max) {
    double x_prev = x_0;
    double v_prev = v_0;
    double x_new, v_new;
    for (double t = 0; t < t_max; t = t   delta) {
        x_new = x_prev   t * v_prev;
        v_new = v_prev - t * x_prev;
        // Writes time, position and velocity into a csv file
        output << std::fixed << std::setprecision(3) << t << "," << x_prev << "," << v_prev << std::endl;
        x_prev = x_new;
        v_prev = v_new;
        // Breaks loop if values get to big
        if ((x_new != x_new) || (v_new != v_new) || (std::isinf(x_new) == true) || (std::isinf(v_new) == true)) {
            break;
        }
    }
}

int main() {
    // Initialize with user input 
    double x_0, v_0, t_max, delta;
    std::cout << "Initial position x0?: ";
    std::cin >> x_0;
    std::cout << "Intial velocity v0?: ";
    std::cin >> v_0;
    std::cout << "Up to what time t_max?: ";
    std::cin >> t_max;
    std::cout << "Step size delta?: ";
    std::cin >> delta;
    // Runs the function
    euler(x_0, v_0, delta, t_max);
}

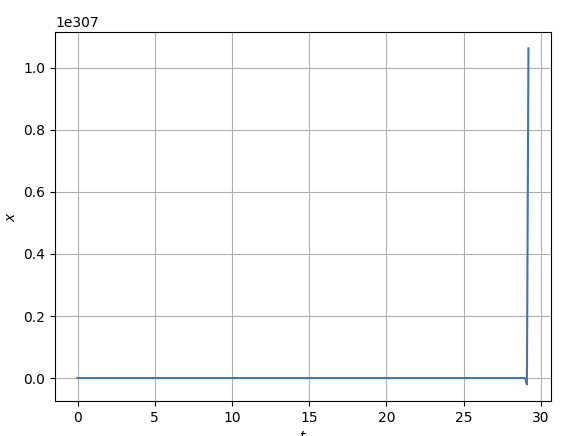
I know that the solution will grow indefinitely but for smaller values of t it should resemble the analytical solution while growing slowly. The values i get are blowing out of proportions after ca. 10 iterations and i can not find out why. When i plot the position as a function of the time i get the plot below, which is obviously wrong.

CodePudding user response：

Your equation implementation is wrong. You are usint t instead of dt. Correct variant:

x_new = x_prev   delta * v_prev;
v_new = v_prev - delta * x_prev;

And a side note if you plan to develop your code further: common approach to implementation of ODE solver is to have a method with signature similar to

Output = solveOde(System, y0, t);

Where System is method that describes the ODE dy/dx = f(x,t), e.g.

std::vector<double> yourSystem(std::vector<double> y, double /*t unused*/)
{
    return {y[1], -y[0]};
}

y0 are initial conditions, and t is a time vector (delta is calculated internally). Take a look at boost odeint or more compact and transparent python documentation.