I am trying to render an outline using Vulkan's stencil buffers. This technique involves rendering the object twice with the second one being scaled up in order to account for said outline. Normally this is done in 3D space in which the normal vectors for each vertex can be used to scale the object correctly. I however am trying the same in 2D space and without pre-calculated normals.

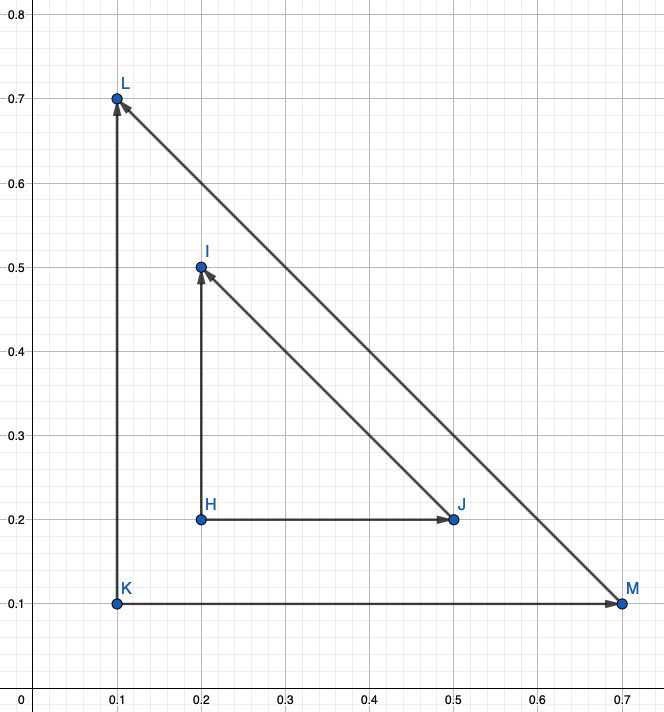
An Example: Given are the Coordinates I, H and J and I need to find L, K and M with the condition that the distance between each set of parallel vectors is the same.

I tried scaling up the object and then moving it to the correct location but that got me nowhere.

I am searching for a solution that is ideally applicable to arbitrary shapes in 2D space and also somewhat efficient. Also I am unsure if this should be calculated on the GPU or the CPU.

CodePudding user response：

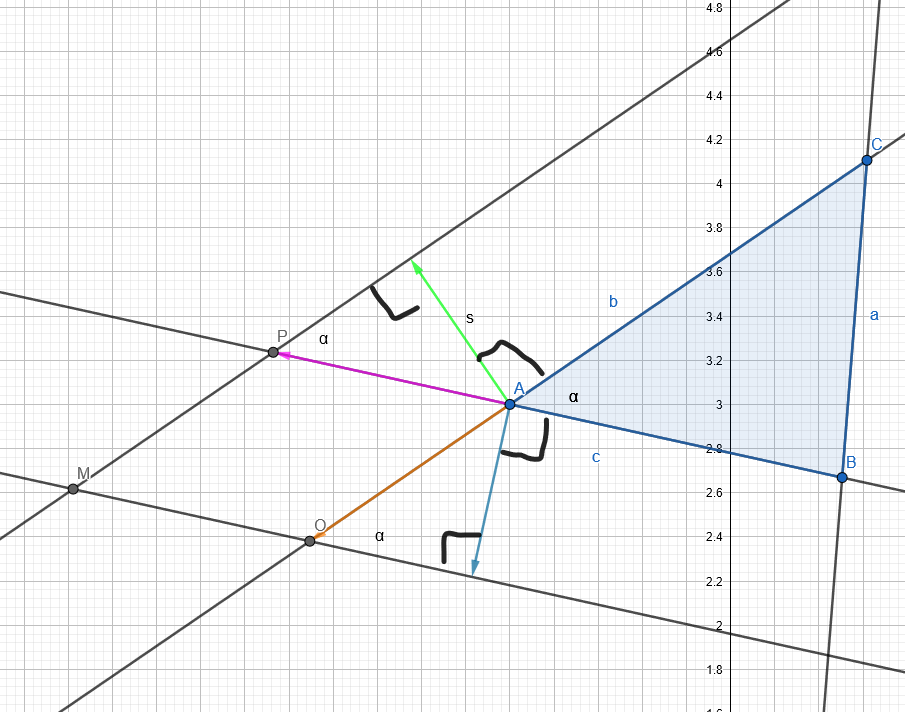
Lets draw an example of a single point of some 2D polygon.

The position of point M depends only on position of A and its two adjacent lines, I have added normals too - green and blue. Points P and Q line on the intersection of a shifted and non-shifted lines.

If we know the adjacent points of A - B , C and the distances to O and P, then

M = A - d_p * normalize(B-A) - d_o * normalize(C-A)

this is true because P, O lie on the lines B-A and C-A.

The distances are easy to compute from the two-color right triangles:

d_p=s/sin(alfa)
d_o=s/sin(alfa)

where s is the desired stencil shift. They are of the course the same.

So the whole computation, given coordinates of A,B,C of some polygon corner and the desired shift s is:

b =  normalize(B-A) # vector
c =  normalize(C-A) # vector
alfa = arccos(b.c)  # dot product
d = s/sin(alfa)
M = A - sign(b.c) * (b c)*d

This also proves that M lies on the alfa angle bisector line.

Anyway, the formula is generic and holds for any 2D polygon, it is easily parallelizible since each point is shifted independently of others. But

• for non-convex corners, you need to use the opposite sign, we can use dot product to generalize.
• It is not numerically stable for b.c close to zero i.e. when b,c lines are almost parallel, in that case I would recommend just shifting A by d*n_b where n_b is the normalized normal of B-A line, in 2D it is normalize((B.y - A.y, A.x-B.x)).