starting values for nls() to solve singular gradient error in R-CodePudding

I am attempting to fit nls() for 520 users to achieve the coefficients of the exponential fitting. The following is a small representation of my data.

dput(head(Mfrq.df.2))
structure(list(User.ID = c("37593", "38643", "49433", "60403", 
"70923", "85363"), V1 = c(9L, 3L, 4L, 80L, 19L, 0L), V2 = c(10L, 
0L, 29L, 113L, 21L, 1L), V3 = c(5L, 2L, 17L, 77L, 7L, 2L), V4 = c(2L, 
2L, 16L, 47L, 4L, 3L), V5 = c(2L, 10L, 16L, 40L, 1L, 8L), V6 = c(4L, 
0L, 9L, 22L, 1L, 7L), V7 = c(6L, 8L, 9L, 8L, 0L, 6L), V8 = c(2L, 
17L, 16L, 24L, 2L, 1L), V9 = c(3L, 20L, 7L, 30L, 0L, 4L), V10 = c(2L, 
11L, 5L, 11L, 2L, 3L)), row.names = c(NA, 6L), class = "data.frame")

Finally, I found two ways of doing this. However for both, I get an error stating singular gradient.

#Way I
x=1:10
Mfrq.df.2_long <- pivot_longer(Mfrq.df.2, matches("V\\d{1,2}"), names_to = NULL, values_to = "Value")

Mfrq.df.2_long %>% 
group_by(User.ID) %>% 
mutate(fit = nls(Value ~ A * exp(k * x), start = c(A =2, k = 0.01)) %>% list())

#Way2
L1 = c()
for (i in unique(Mfrq.df.2$User.ID)) {L1[[as.character(i)]]=seq(1,10)}
length(L1) #520 users
dput(head(L1))

list(`37593` = 1:10, `38643` = 1:10, `49433` = 1:10, `60403` = 1:10, 
    `70923` = 1:10, `85363` = 1:10)

#Way 2 Continue
L2=list.ids.RecSOC.2
length(L2) #520 users
dput(head(L2))

list(`37593` = c(9L, 10L, 5L, 2L, 2L, 4L, 6L, 2L, 3L, 2L), `38643` = c(3L, 
0L, 2L, 2L, 10L, 0L, 8L, 17L, 20L, 11L), `49433` = c(4L, 29L, 
17L, 16L, 16L, 9L, 9L, 16L, 7L, 5L), `60403` = c(80L, 113L, 77L, 
47L, 40L, 22L, 8L, 24L, 30L, 11L), `70923` = c(19L, 21L, 7L, 
4L, 1L, 1L, 0L, 2L, 0L, 2L), `85363` = c(0L, 1L, 2L, 3L, 8L, 
7L, 6L, 1L, 4L, 3L))

#Way 2 Continue    
control=nls.control(maxiter=1000)
res <- mapply(function(x,y){
  nls(y~A*(exp(-k*x)),
      start=list(A=100, k=0.01), control=control,
      trace= TRUE, data=data.frame(x, y))},L1,L2, SIMPLIFY=FALSE)

To the best of my understanding, it has something to do with the starting values. I find it hard to find starting values that would work for all 520. Especially knowing not all of them are following the defined curve. I still need all 520 coefficients (A&k) to do my further analyses.

Any recommendations? Thanks

CodePudding user response：

The starting values are very important with nls() so you need to spend some time getting them right. First let's extract the first group:

Value <- unlist(Mfrq.df.2_long[Mfrq.df.2_long$User.ID==37593, "Value"])
x <- 1:10
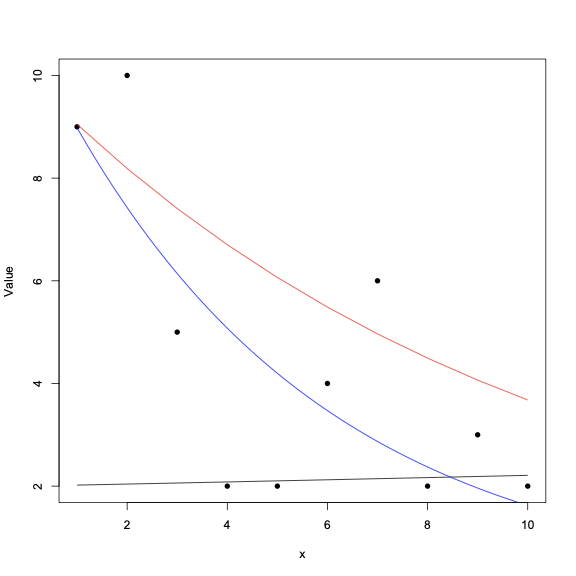
plot(x, Value)

This plot shows declining values from about 10 to 2 on the Y axis as the x values range from 1 to 10. What do your starting values look like on this plot?

Y <- 2 * exp(.01 * x)
lines(x, Y)

A very slightly increasing value from 2 to 2.2 over the range of x. Clearly the value inside exp() must be negative and greater than .01 since the decline is much greater than your starting values and the starting value for A should be more like 10:

Y <- 10 * exp(-.1 * x)
lines(x, Y, col="red")

This is much better. Now nls():

# fit = nls(Value ~ A * exp(k * x), start = c(A = 10, k = -.1))
# fit
# Nonlinear regression model
#   model: Value ~ A * exp(k * x)
#    data: parent.frame()
#       A       k 
# 10.8628 -0.1901 
#  residual sum-of-squares: 33.66
# 
# Number of iterations to convergence: 7 
# Achieved convergence tolerance: 9.325e-06

Plotting the result:

xfit <- seq(1, 10, by=.1)
yfit <- predict(fit, list(x=xfit))
lines(xfit, yfit, col="blue")

Once you get the first group to work, it should be straightforward to apply it to the rest of the groups.

CodePudding user response：

One option to estimate the coefficients is to perform a linear regression on a transformed data set.

y = A*exp(kx)
can be transformed to
ln(y) = kx B

Mfrq.df.2_long <- pivot_longer(Mfrq.df.2, matches("V\\d{1,2}"), names_to = NULL, values_to = "Value")

data <- Mfrq.df.2_long[Mfrq.df.2_long$User.ID==37593, ]
#Add the independent value to data frame
data$x <- 1:10

#fit linear model ln(y)= A*x  B
model <- lm(log(Value) ~ x, data)
#predict(model, data.frame(x))

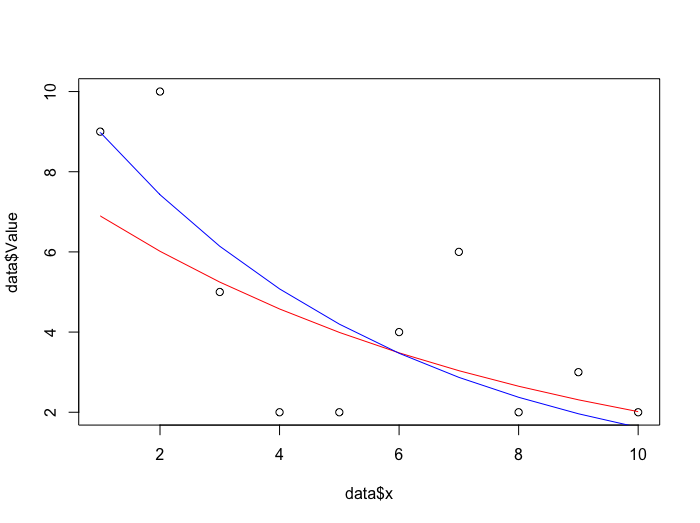
#plot original data
plot(data$x, data$Value)
#plot linear model 
#taking the exp of the prediction since the model was to preduct ln(y)
lines(data$x, exp(predict(model, data.frame(x=1:10))), col="red")

#Extract out the coefficients A=exp(intercept) from linear model 
# And set the start values 
sA <- exp(model$coefficients[1])
sk <- model$coefficients[2]
model2 <- nls(Value ~ A * exp(k * x), data= data, start = list(A = sA, k = sk))

#plot the nls model
lines(data$x, predict(model2, data.frame(x=1:10)), col="blue")

Note: the equations are slightly different be the least squares is typing to minimize the differences between different values y and ln(y).