How to transform (rotate, scale etc.) an entity without structural change in Unity DOTS-CodePudding

I actually try to rotate objects that are described as an Entity in Unity Dots. I know there are Rotation components to do so. But the entities do not automatically have it, when I create them from Mesh. So if I add it manually, it will trigger structural changes, which might be very bad for performance.

They all have LocalToWorld, which contains a matrix, but I do actually not understand the matrix and could not find good articles what they mean and how to work with it.

CodePudding user response：

After spending a lot of time trying to understand the matrix, I finally found the solution. If you are like me, that geometry is really not one of my strengths, I will tell you the solution that I found, and for the ones interested in, explain how the matrix actually work.

Now for my question to rotate the Entity, this is the solution:

float angleInDegrees = 90f;
Entities.ForEach((ref LocalToWorld localToWorld) => {
    float4x4 rotationMatrix = float4x4.RotateZ(math.radians(angleInDegrees));
    rotationMatrix.c3 = position.Value.c3;
    localToWorld.Value = rotationMatrix;
});

You might also use it with float4x4.Scale etc. If you are only interested in how to do it, that's it.

Meaning of the matrix

First of all, the matrix consists of 4x4 instead of 3x3, because it's using Homogeneous Coordinates (What this is, is described down below).

Now let's look at that picture (from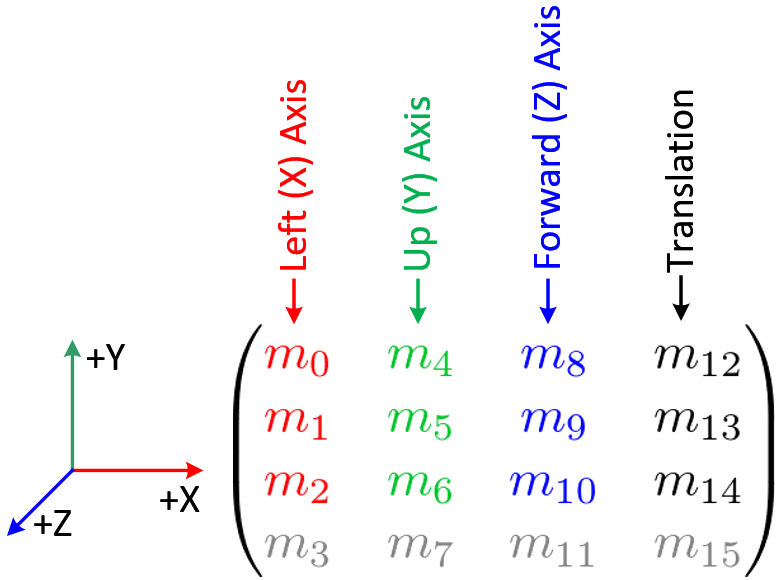

The last column of the matrix describes the actual position of the object in world space. Where m12=x, m13=y, m14=z. The last row contains the w part of the coordinates, which is described below (in Homogeneous Coordinates). The first three columns describe how the coordinates of the last column (so the position of the object) are translated to final coordinates like with a regular matrix (If you are not familiar with matrices, I describe it down below).

Now what is special, is the following: The last column is the position in world space. The first three rows define the transformation in local space. So if you want to rotate the object around it's centered z axis you just use it like that:

Matrix conversions

For explanation let's take a very simple example in 2D space (with cartesian coordinates, so no w part).

If you have a point or vector X/Y, let's say 4/3, then the matrix describes, how these coordinates are affected to get the result.

This is how the calculation is done:

     Xin Yin      Point          Result
Xout  m0  m2   *    x    =>  (m0 * x   m2 * y)
Yout  m1  m3        y        (m1 * x   m2 * y)

So m0 describes, how much x of the input (point or vector) affects the x coordinate of the result, m1 how much x affects the y coordinate of the result etc.

So if want to keep the point exactly as is, then you would take this matrix (it's called identity)

     Xin Yin      Point                        Result
Xout  1   0   *     4    =>  1 * 4   0 * 3   =>  4
Yout  0   1         3        0 * 4   1 * 3       3

If you want to rotate your point or vector by 270° clockwise, you would use this matrix

     Xin Yin      Point                        Result
Xout  0   1   *     4    =>  0 * 4   1 * 3   =>  3
Yout -1   0         3       -1 * 4   0 * 3      -4

Homogeneous Coordinates

I'll only explain how they work. If you want to know the reason to use them, or do not understand my explanation, then you probably might want to take a look at that post.

Homogeneous over cartesian coordinates add an extra point to the dimensions you already have (so for 2D 3 points, for 3D 4 points etc.). A 3D vector with homogeneous coordinates would be described as (x, y, z, w).

The conversion is done by:

Cartesian       Homgeneous
(x, y, z) <=> (x/w, y/w, z/w)

So if you want to convert a float3 to float4, you just add 1 as w (new float4(cartesianCoordinate, 1f)). If you want to convert it back, you do (float3)(homogeneousCoordinate / homogeneousCoordinate.w)

I hope this helps you to save the time I spent ;-)