Hello everyone I want to make a matrix that looks like the image, what I did first was to create a matrix of zeros and then with a for I made the diagonal of the matrix but now I need to make the diagonals that are above and below the -2 but in those there is not a single value, those have zeros and ones so I am not very clear how to make them.
try to make them with this code
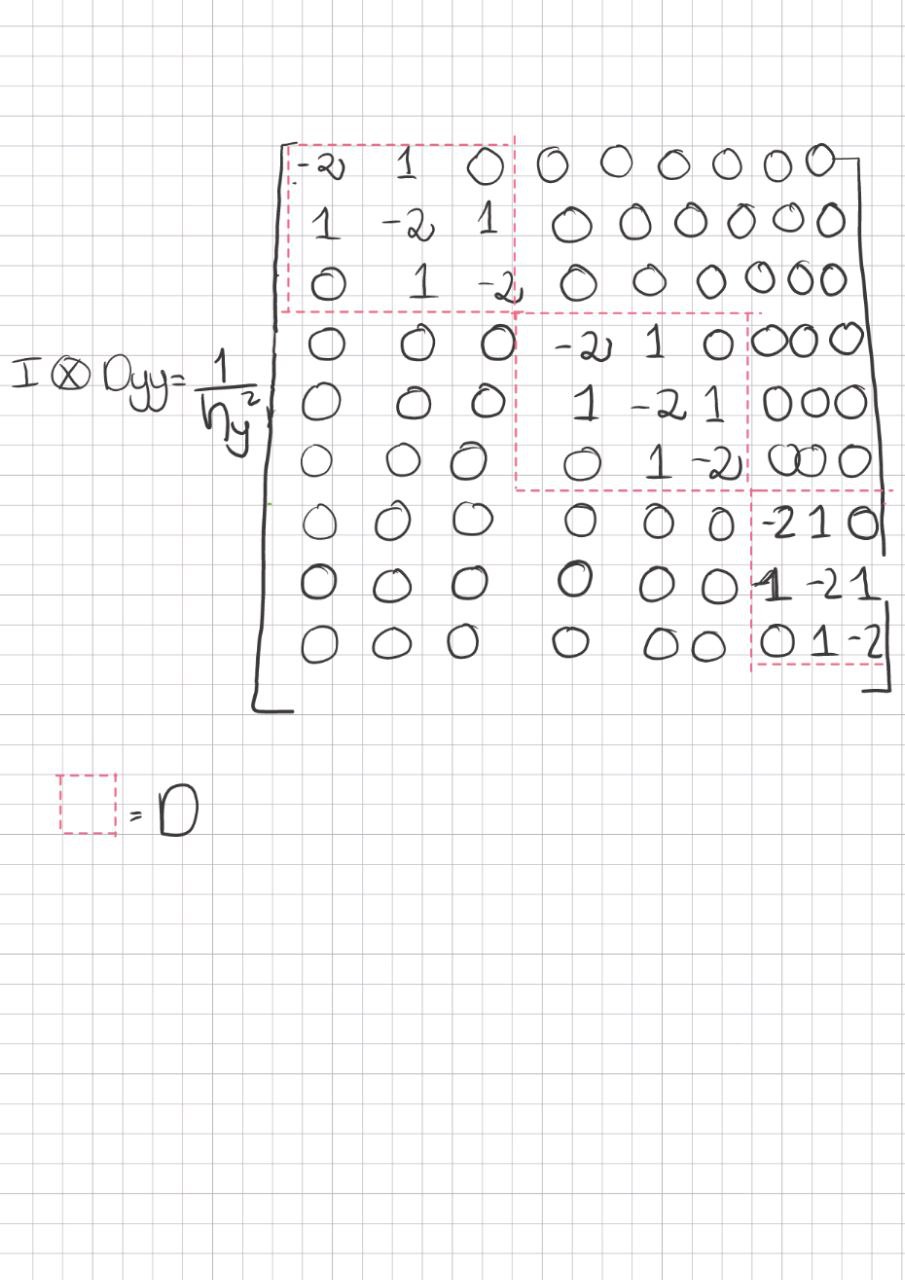
N=3
D2=np.zeros((N**2,N**2))
for i in range(N**2):
for j in range(N**2):
if i==j:
D2[i,j]=-2
elif np.abs(i-j)==1:
D2[i,j]=1
CodePudding user response:
One way is to build it from diagonals. Short answer
m=np.roll(np.diag(([1]*(N-1) [0])*N), 1)-np.identity(N**2)
m m.T
Explanation
np.diag(([1]*(N-1) [0])*N)
is
array([[1, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 1, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0]])
If you roll it 1 (rightwise)
np.roll(np.diag(([1]*(N-1) [0])*N), 1)
array([[0, 1, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0, 0, 0, 0]])
If we remove identity from that
m=np.roll(np.diag(([1]*(N-1) [0])*N), 1)-np.identity(N**2)
m
array([[-1, 1, 0, 0, 0, 0, 0, 0, 0],
[ 0, -1, 1, 0, 0, 0, 0, 0, 0],
[ 0, 0, -1, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, -1, 1, 0, 0, 0, 0],
[ 0, 0, 0, 0, -1, 1, 0, 0, 0],
[ 0, 0, 0, 0, 0, -1, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, -1, 1, 0],
[ 0, 0, 0, 0, 0, 0, 0, -1, 1],
[ 0, 0, 0, 0, 0, 0, 0, 0, -1]])
We are halfway. We need to double diagonal, and add the symmetric one. Which we can do it easily
m m.T
array([[-2, 1, 0, 0, 0, 0, 0, 0, 0],
[ 1, -2, 1, 0, 0, 0, 0, 0, 0],
[ 0, 1, -2, 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, -2, 1, 0, 0, 0, 0],
[ 0, 0, 0, 1, -2, 1, 0, 0, 0],
[ 0, 0, 0, 0, 1, -2, 0, 0, 0],
[ 0, 0, 0, 0, 0, 0, -2, 1, 0],
[ 0, 0, 0, 0, 0, 0, 1, -2, 1],
[ 0, 0, 0, 0, 0, 0, 0, 1, -2]])
CodePudding user response:
You've got several choices....
You could "hand jam" the whole thing in by just typing the rows. (You probably already know this.)
D = [[-2, 1, 0, ...], [...]]
You can make a smaller matrix that represents what you have in the red-dashed box (the sub-matrix) and just replace values in
Dby over-writing them with the appropriate ranges in D as such ( you could make a little loop to hit the right indices for replacement by stepping by 3...) (not shown):
In [30]: D
Out[30]:
array([[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0., 0., 0., 0., 0.]])
In [31]: temp = [[-2, 1, 0],
...: [1, -2, 1],
...: [0, 1, -2]]
In [32]: D[0:3,0:3] = temp
In [33]: D
Out[33]:
array([[-2., 1., 0., 0., 0., 0., 0., 0., 0.],
[ 1., -2., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 1., -2., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.]])
- You can look for a pattern in where the zeros land and augment your loop. In this case, every zero location is a total of 6 moves away from a previous zero (3 over, 3 down), so if we can anchor the first zero, we can use a modulo operator to zero out every other occurrence that is 6 moves away. The first zero is 5 moves away from the origin at (2,3) (or equivalently (3, 2) so:
In [34]: D = np.zeros((n,n))
In [35]: for i in range(n):
...: for j in range(n):
...: if i==j:
...: D[i,j]=-2
...: elif np.abs(i-j)==1:
...: if (i j-5) % 6 == 0:
...: D[i,j]=0
...: else:
...: D[i,j]=1
...:
In [36]: D
Out[36]:
array([[-2., 1., 0., 0., 0., 0., 0., 0., 0.],
[ 1., -2., 1., 0., 0., 0., 0., 0., 0.],
[ 0., 1., -2., 0., 0., 0., 0., 0., 0.],
[ 0., 0., 0., -2., 1., 0., 0., 0., 0.],
[ 0., 0., 0., 1., -2., 1., 0., 0., 0.],
[ 0., 0., 0., 0., 1., -2., 0., 0., 0.],
[ 0., 0., 0., 0., 0., 0., -2., 1., 0.],
[ 0., 0., 0., 0., 0., 0., 1., -2., 1.],
[ 0., 0., 0., 0., 0., 0., 0., 1., -2.]])
