Can someone explain to me the code that is in the

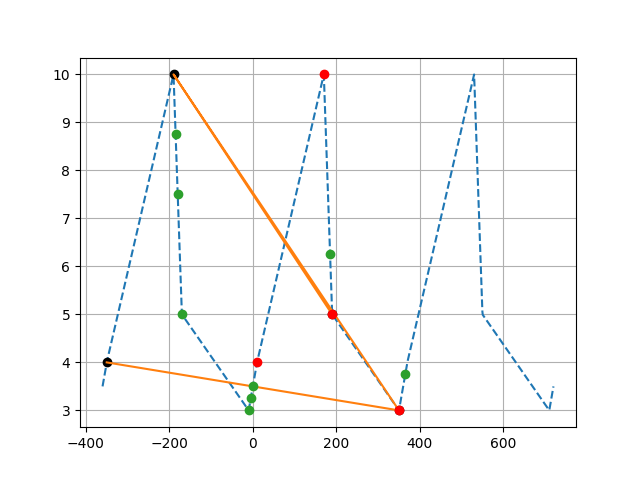
How the orange points can be considered "interpolations" is beyond me. They are not even in the curve

EDIT: Thanks to Warren Weckesser for the detailed explanation! A plot to see it better

CodePudding user response：

The numbers used in the example that demonstrates the use of period in the interp docstring can be a bit difficult to interpret in a plot. Here's what is happening...

The period is 360, and the given "known" points are

xp = [190, -190, 350, -350]
fp = [  5,   10,   3,    4]

Note that the values in xp span an interval longer than 360. Let's consider the interval [0, 360) to be the fundamental domain of the interpolator. If we map the given points to the fundamental domain, they are:

xp1 = [190, 170, 350, 10]
fp1 = [  5,  10,   3,  4]

Now for a periodic interpolator, we can imagine this data being extended periodically in the positive and negative directions, e.g.

xp_ext = [..., 190-360, 170-360, 350-360, 10-360, 190, 170, 350, 10, 190 360, 170 360, 350 360, 10 360, ...]
fp_ext = [...,       5,      10,       3,      4,   5,  10,   3,  4,       5,      10,       3,      4, ...]

It is this extended data that interp is interpolating.

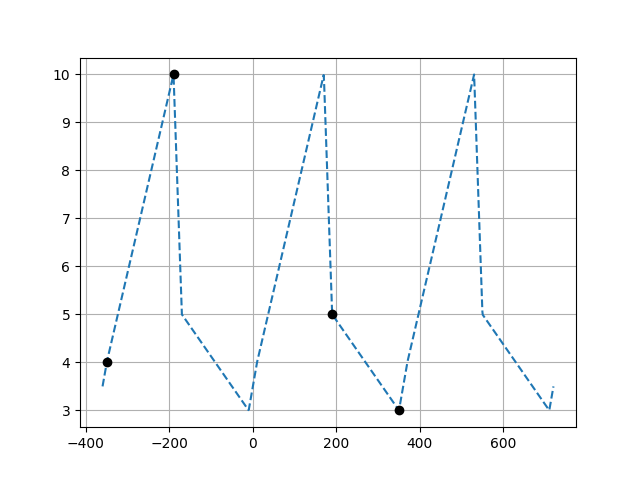
Here's a script that replaces the array x from the example with a dense set of points. With this dense set, the plot of y = np.interp(x, xp, fp, period=360) should make clearer what is going on:

xp = [190, -190, 350, -350]
fp = [5, 10, 3, 4]
x = np.linspace(-360, 720, 1200)
y = np.interp(x, xp, fp, period=360)
plt.plot(x, y, '--')
plt.plot(xp, fp, 'ko')
plt.grid(True)

Each "corner" in the plot is at a point in the periodically extended version of (xp, fp).