Find the closest point to a line from an array of points-CodePudding

I have the problem of finding the point which is closest to a line from an array of x- and y-data. The line is given as an angle from the origin at (0,0). The x,y data of the points is given in relation to the origin.

How do I find the closest point (and its distance) to the line?

This is an example of the data I have:

  import numpy as np
  import matplotlib.pyplot as plt

  def main():
    depth = np.random.random((100))*20 50
    angle = np.linspace(0, 2*np.pi, 100)
    x,y = depth2xy(depth, angle)

    line = np.random.random_sample()*2*np.pi

    # fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
    plt.scatter(x, y)
    plt.plot([0,100*np.cos(line)], [0, 100*np.sin(line)], markersize=10, color = "r")
    plt.show()

  def depth2xy(depth, angle):
    x, y = np.zeros(len(depth)), np.zeros(len(depth))
    for i in range(len(depth)):
      x[i] = depth[i]*np.cos(angle[i])
      y[i] = depth[i]*np.sin(angle[i])
    return x,y

  if __name__ == "__main__": main()

I could try a brute force approach, iterating over different distances along the line to find the ultimate smallest distance.

But as time efficiency is critical my case and the algorithm would not perform as well as I think it could, I would rather try an analytical approach.

I also thought about scipy.spatial.distance, but I am not sure how this would work for a line.

CodePudding user response：

Let P be a point from your know data set. Let Q be the projection of this point on the line. You can use an analytic approach to determine the exact location of Q:

OQ is the segment from the origin to the Q point. It is aligned to the line.
PQ is the distance of the point P to the line.
from geometry, the dot product between QP and OQ is zero (the two segments are orthogonal to each other). From this equation we can compute the point Q.

After that, you simply compute all distances and find the shortest one.

I'm going to use SymPy for the analytical part, Numpy for the numerical part and Matplotlib for plotting:

from sympy import *
import numpy as np
import matplotlib.pyplot as plt

xq, xp, yq, yp, m = symbols("x_Q, x_P, y_Q, y_P, m")
A = Matrix([xq - xp, yq - yp])
B = Matrix([xq, yq])
# this equations contains two unkowns: xq, yq
eq = A.dot(B)

# but we know the line equation: yq = m * xq, so we substitute it into
# eq and solve for xq
xq_expr = solve(eq.subs(yq, m * xq), xq)[1]
print(xq_expr)
# (m*y_P   x_P)/(m**2   1)

# generate data
mv = -0.5
xp_vals = np.random.uniform(2, 10, 30)
yp_vals = np.random.uniform(2, 10, 30)

# convert the symbolic expression to a numerical function
f = lambdify([m, xp, yp], xq_expr)
# compute the projections on the line
xq_vals = f(mv, xp_vals, yp_vals)
yq_vals = mv * xq_vals

# compute the distance
d = np.sqrt((xp_vals - xq_vals)**2   (yp_vals - yq_vals)**2)
# find the index of the shortest distance
idx = d.argmin()

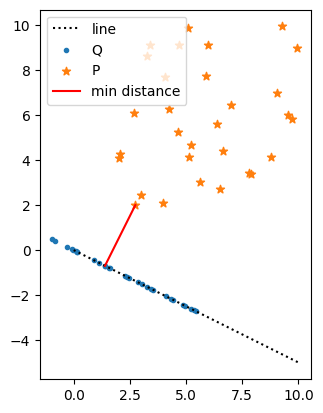
fig, ax = plt.subplots()
xline = np.linspace(0, 10)
yline = mv * xline
ax.plot(xline, yline, "k:", label="line")
ax.scatter(xq_vals, yq_vals, label="Q", marker=".")
ax.scatter(xp_vals, yp_vals, label="P", marker="*")
ax.plot([xp_vals[idx], xq_vals[idx]], [yp_vals[idx], yq_vals[idx]], "r", label="min distance")
ax.set_aspect("equal")
ax.legend()
plt.show()

CodePudding user response：

Your assigned line passes through the origin, its parametric equation is

x = u cos(a)
y = u sin(a)

and you can see the parameter u is simply the (oriented) distance beteween the origin and a point on the assigned line.

Now, consider a point of coordinates X and Y, a line perpendicular to the assigned one has the parametric equation

x = X - v sin(a)
y = Y   v cos(a)

and again, the parameter v is simply the (oriented) distance between (X, Y) and a point on a line passing per (X, Y) and perpendicular to the assigned one.

The intersection is given by the equation

X = u cos(a)   v sin(a)
Y = u sin(a) - v cos(a)

you can check by inspection that the solution of the system is

u = X cos(a)   Y sin(a)
v = X sin(a) - Y cos(a)

The distance of the point (X, Y) from the assigned line is hence

d = | X sin(a) - Y cos(a) |