banknotes provided = 10 Dollar, 50 Dollar, 100 Dollar
Expected Result for 100 dollar bill with above bank notes. I want to show the denomination exactly like below
10 x 10
1 x 50 5 x 10
2 x 50
1 x 100
As you can see all the banknotes denomination total to 100 above
My code show far , I feel i need to use recursion. Thanks for having a look.
int[] noOfBankNotes = {10, 50, 100};
int amount = 100;
int j = 0;
int k = 0;
string strValue = "";
for (int i = 0; i < noOfBankNotes.Length; i ) {
j = amount / noOfBankNotes[i];
k = j * noOfDenomination[i];
amount = amount % noOfBankNotes[i];
if (k != 0) {
strValue = strValue j "*" noOfBankNotes[i] "=" k;
}
}
Console.WriteLine(strValue);
CodePudding user response:
Let's split the problem in two:
- Solve the exchange problem of
totalgivennotes(in descending order), starting from nominal atindex. - Provide the solution in required format
Code:
private static IEnumerable<int[]> Solutions(int total, int[] notes, int index) {
int value = notes[index];
if (index == notes.Length - 1) {
if (total % value == 0)
yield return new int[] { total / value };
}
else
for (int i = total / value; i >= 0; --i)
foreach (int[] rest in Solutions(total - value * i, notes, index 1))
yield return rest.Prepend(i).ToArray();
}
private static IEnumerable<string> Solve(int total, int[] notes) {
var items = notes.OrderByDescending(item => item).ToArray();
foreach (int[] solution in Solutions(total, items, 0))
yield return string.Join(" ", solution
.Zip(items, (count, note) => (count, note))
.Where(pair => pair.count > 0)
.Select(pair => $"{pair.count} x {pair.note}"));
}
Demo:
int total = 170;
int[] notes = new int[] {10, 50, 100};
Console.Write(string.Join(Environment.NewLine, Solve(total, notes)));
Output:
1 x 100 1 x 50 2 x 10
1 x 100 7 x 10
3 x 50 2 x 10
2 x 50 7 x 10
1 x 50 12 x 10
17 x 10
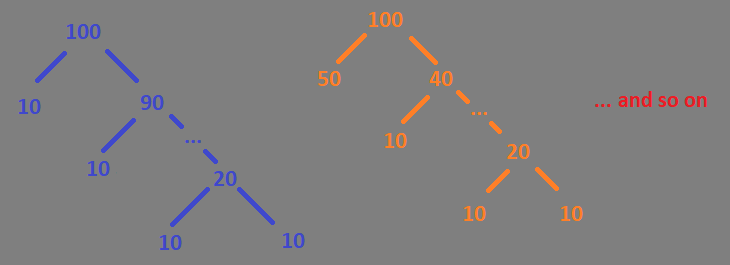
The leaf values then get transformed to your output, and possible duplicates (since different trees can be created from the same bank notes) are not printed out.
The following input:
int[] availableBanknotes = { 10, 50, 100 };
int amount = 100;
SolveRecursive(amount, availableBanknotes);
prints out:
10 x 10
1 x 50 5 x 10
2 x 50
1 x 100
The following input:
int[] availableBanknotes = { 10, 50, 100 };
int amount = 170;
SolveRecursive(amount, availableBanknotes);
prints out:
17 x 10
1 x 50 12 x 10
2 x 50 7 x 10
1 x 100 7 x 10
3 x 50 2 x 10
1 x 100 1 x 50 2 x 10
Here is the code:
private static List<string> Solutions = new List<string>();
private static void SolveRecursive(int amount, int[] availableBanknotes)
{
List<int> denomination = new List<int>();
for (int i = 0; i < availableBanknotes.Length; i )
{
if (amount >= availableBanknotes[i])
{
ProvidedBanknotes(amount, availableBanknotes[i], availableBanknotes, new List<int>(denomination));
}
}
Solutions = new List<string>();
}
private static void ProvidedBanknotes(int amount, int currentBankNote, int[] availableBanknotes, List<int> denomination)
{
amount = amount - currentBankNote;
denomination.Add(currentBankNote);
if (amount == 0)
{
PrintSolution(denomination, availableBanknotes);
return;
}
for (int i = 0; i < availableBanknotes.Length; i )
{
if(amount >= availableBanknotes[i])
{
ProvidedBanknotes(amount, availableBanknotes[i], availableBanknotes, new List<int>(denomination));
}
}
}
private static void PrintSolution(List<int> denomination, int[] availableBanknotes)
{
string solution = "";
for(int i = availableBanknotes.Length - 1; i >= 0; i--)
{
int currentVal = availableBanknotes[i];
int count = denomination.Where(temp => temp.Equals(currentVal))
.Select(temp => temp)
.Count();
if (count != 0)
{
if(solution.Equals(""))
{
solution = $"{count} x {currentVal}";
}
else
{
solution = solution $" {count} x {currentVal}";
}
}
}
if(!Solutions.Contains(solution))
{
Solutions.Add(solution);
Console.WriteLine(solution);
}
}
CodePudding user response:
Given
var notes = new[] { 10, 50, 100 };
var total = 100;
You can use a LINQ Extension Method to create all possible combinations of notes and filter them to just combinations that could be used to create the total. I sort the notes in the combination descending so that the final answer will be output in descending order:
var possibleCombos = notes.Where(n => n <= total)
.AllCombinations()
.Select(c => c.OrderByDescending(n => n).ToList())
.Where(c => c.Sum() <= total && c.Aggregate(total-c.Sum(), (r, n) => r % n) == 0)
.OrderBy(c => c.Last());
While it doesn't apply to the example, the Aggregate expression ensures that impossible combinations aren't selected, such as trying to make { 50, 20 } yield 100.
For each possible combination, you can start with the total and then take away one of each note to ensure at least one of each note is in the answer. It then computes the number of additional notes needed for each denomination, starting with the largest. For each combination it outputs the number of each note in the format requested:
foreach (var combo in possibleCombos) {
var numberOfNotes = Enumerable.Repeat(1, combo.Count).ToList(); // one of each denomination
var remainder = total - combo.Sum(); // start by taking away one of each denomination
for (int j1 = 0; j1 < combo.Count; j1) {
numberOfNotes[j1] = remainder / combo[j1]; // take away all possible of each denomination
remainder = remainder % combo[j1];
}
Console.WriteLine(String.Join(" ", numberOfNotes.Select((numberOfNote, j1) => $"{numberOfNote} x {combo[j1]}")));
}
The extension method is defined as:
public static class IEnumerableExt {
public static IEnumerable<IEnumerable<T>> AllCombinations<T>(this IEnumerable<T> start) {
IEnumerable<IEnumerable<T>> HelperCombinations(IEnumerable<T> items) {
if (items.IsEmpty())
yield return items;
else {
var head = items.First();
var tail = items.Skip(1);
foreach (var sequence in HelperCombinations(tail)) {
yield return sequence; // Without first
yield return sequence.Prepend(head);
}
}
}
return HelperCombinations(start).Skip(1); // don't return the empty set
}
}
NOTE: This only produces one possible solution for each combination of bills, the one that uses the maximum possible number of the largest denomination.