I have a function with exponentials :

f = function(x){
  exp(3*x) 4*exp(2*x)-3*exp(x)
}

this function has one real root which is $\sqrt(7)-2$ or 0.6457513 as discussed

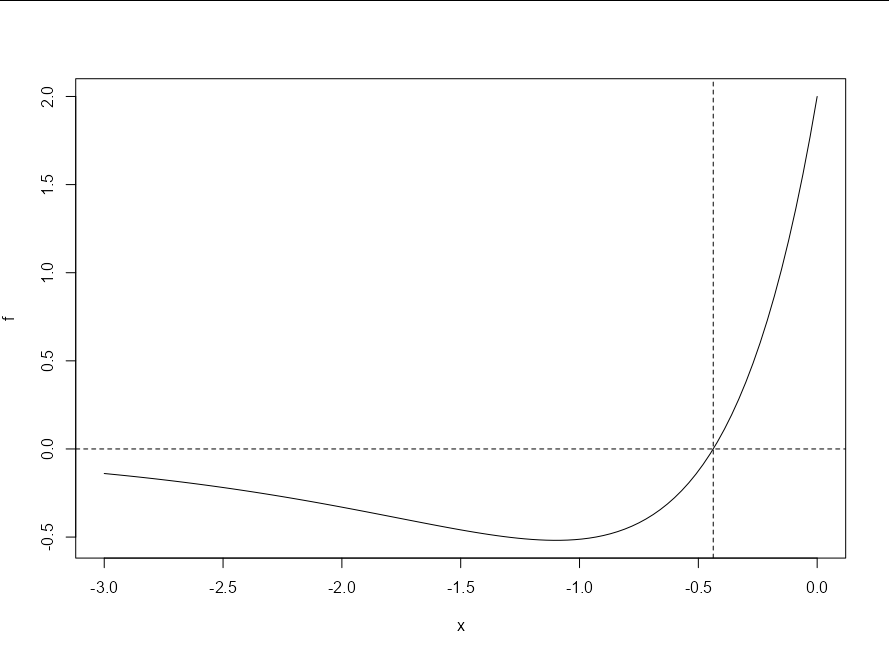
Note that there is a single root somewhere between -1 and 0. If we draw a vertical line at the uniroot solution, it should coincide with the point where the line crosses the x axis:

abline(v = uniroot(f, lower = -1, upper = 0)$root, lty = 2)

Note that it's easy to confirm whether the value 0.6457513 is a root by passing it to your function. This returns:

f(0.6457513)
#> [1] 15.77041

Which tells us this is not a root.

If you look at the answer on math overflow, they show that t = sqrt(7) - 2, but remember t was substituted for exp(x), so exp(x) = sqrt(7) - 2, and therefore the root is at x = log(sqrt(7) - 2)

log(sqrt(7) - 2)
#> [1] -0.4373408

If we feed this number into your function we can see that it is indeed a root (within the limits of floating point arithmetic)

f(log(sqrt(7) - 2))
#> [1] 4.440892e-16