How is position wise feed forward neural network implemented for transformers?-CodePudding

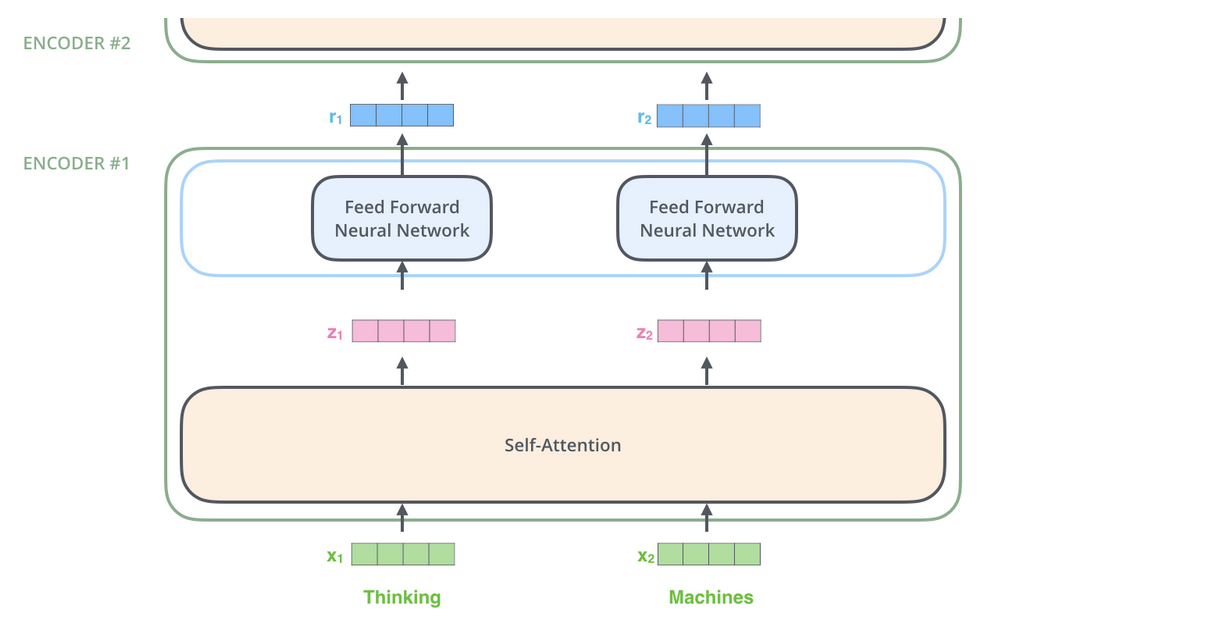
I am having hard time understanding position wise feed forward neural network in transformers architecture.

Lets take example as Machine translation task, where inputs are sentences. From the figure I understand that for each word, different feed forward neural network is used to the output of self attention sub-layer. The feed forward layer apply similar Linear transformations but actual weights and biases for each transformations are different because they are two different feed forward neural network.

refering to Link, Here is the class for PositionWiseFeedForward neural network

class PositionwiseFeedForward(nn.Module):
    "Implements FFN equation."
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(F.relu(self.w_1(x))))

My question is:

I don't see anything position-wise about this. This is simple fully connected neural network with two layers. assuming x to be list of embedding of each word in a sentence, each word in a sentence is transformed by above layer using same set of weight and biases.(correct me if i am wrong)

I was expecting to find something like passing each word embedding to separate Linear layer which will have different weight and biases to achieve something similar to what is shown in the picture.

CodePudding user response：

It is indeed just a single feedforward network rather than a separate one for each position. I don’t know why the paper says “position-wise”. As you said, there’s nothing really position-wise here.

CodePudding user response：

The weights are shared for a layer. After self-attention, all the transformed vectors are assumed to be in the same vector space. So, the same type of transformation can be applied to each of those vectors. This intuition is also used in some other tasks like sequence labelling where each token share the same classification head. This reduces the parameters of the network and forces the self-attention to do the heavy lifting.

Quoting from the link you provided,

While the linear transformations are the same across different positions, they use different parameters from layer to layer.

The x passed in the forward function is a single word vector z_i, not a list.