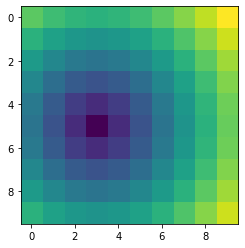
I have a 2D NumPy array of size 10 by 10, in which I am trying to implement a 2D Gaussian distribution on it so that I can use the new column as a feature in my ML model. The center (the peak of the Gaussian distribution) should be at (3, 5) of the 2D NumPy array. Is there any way to do this in Python? I have also included a heatmap of my np array. I appreciate any feedback! Happy New Year!
Here is my data:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
my_np_list = [310.90634 , 287.137 , 271.87973 , 266.6 , 271.87973 ,
287.137 , 310.90634 , 341.41458 , 377.02936 , 416.44254 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
159.96 , 106.64001 , 53.320004, 0. , 53.320004,
106.64001 , 159.96 , 213.28001 , 266.6 , 319.92 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ]
my_np_array = np.array(my_np_list).reshape(10, 10)
plt.imshow(my_np_array, interpolation='none')
plt.show()
size = 100
store_center = (3, 5)
i_center = 3
j_center = 5
I tried the scipy.stats.multivariate_normal.pdf on my array, but it didn't work.
import scipy
from scipy import stats
my_np_array = my_np_array.reshape(-1)
y = scipy.stats.multivariate_normal.pdf(my_np_array, mean=2, cov=0.5)
y = y.reshape(10,10)
yy = np.dot(y.T,y)
CodePudding user response:
If I understand your question correctly, you'd like to calculate a 2D Gaussian PDF with the same shape (e.g. 10 by 10) of the data you have in my_np_array. The provided code calculates a 1D distribution as the input array is reshaped to 1D, with only one relevant mean value, and one cov value. Instead, create a grid of index values (all i, j pairs), and use i_center and j_center as the two mean values of the 2D distribution along the i and j dimensions, respectively:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
my_np_list = [310.90634 , 287.137 , 271.87973 , 266.6 , 271.87973 ,
287.137 , 310.90634 , 341.41458 , 377.02936 , 416.44254 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
159.96 , 106.64001 , 53.320004, 0. , 53.320004,
106.64001 , 159.96 , 213.28001 , 266.6 , 319.92 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ]
my_np_array = np.array(my_np_list).reshape(10, 10)
plt.imshow(my_np_array, interpolation='none')
plt.show()
i_center = 3
j_center = 5
# Create grid of i, j points
# See https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.multivariate_normal.html
j_n, i_n = my_np_array.shape
j_grid, i_grid = np.mgrid[0:j_n, 0:i_n]
pos = np.dstack((j_grid, i_grid))
# Create 2D Gaussian PDF values for grid
rv = multivariate_normal([j_center, i_center], [[0.5, 0], [0, 0.5]])
y = rv.pdf(pos)
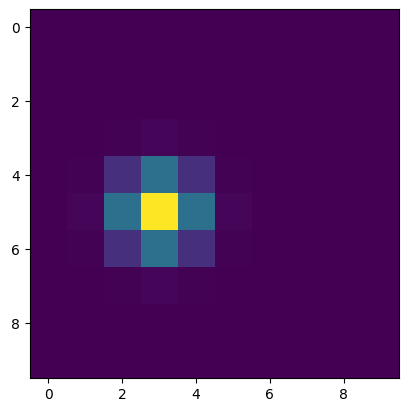
# Plot 2D PDF values
plt.imshow(y, interpolation='none')
plt.show()
The pdf is evaluated over all the j and i pairs in pos, and the j_center and i_center values provide the position where the peak in the 2D Gaussian distribution occurs (i.e. the mean values). The cov matrix only has the one value provided on the diagonals as it looks like the data has the same cov along the j and i axes.
CodePudding user response:
Here is a 2-Gaussian of best fit.
import numpy as np
import matplotlib.pyplot as plt
import scipy.optimize
my_np_list = [
310.90634 , 287.137 , 271.87973 , 266.6 , 271.87973 ,
287.137 , 310.90634 , 341.41458 , 377.02936 , 416.44254 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
159.96 , 106.64001 , 53.320004, 0. , 53.320004,
106.64001 , 159.96 , 213.28001 , 266.6 , 319.92 ,
168.61266 , 119.22715 , 75.40587 , 53.320004, 75.40587 ,
119.22715 , 168.61266 , 219.844 , 271.87973 , 324.33292 ,
192.248 , 150.81174 , 119.22715 , 106.64001 , 119.22715 ,
150.81174 , 192.248 , 238.4543 , 287.137 , 337.2253 ,
226.2176 , 192.248 , 168.61266 , 159.96 , 168.61266 ,
192.248 , 226.2176 , 266.6 , 310.90634 , 357.68146 ,
266.6 , 238.4543 , 219.844 , 213.28001 , 219.844 ,
238.4543 , 266.6 , 301.62347 , 341.41458 , 384.496 ,
]
my_np_array = np.array(my_np_list).reshape(10, -1)
def gaussian2(xy: np.ndarray, a: float, b: float, c: float, d: float, e: float, f: float) -> np.ndarray:
x, y = xy
z = (
a - b
* np.exp(-((x - c)/d)**2)
* np.exp(-((y - e)/f)**2)
)
return z
xy = np.stack(
np.meshgrid(
np.arange(my_np_array.shape[1]),
np.arange(my_np_array.shape[0]),
)
).reshape((2, -1))
param, _ = scipy.optimize.curve_fit(
f=gaussian2,
xdata=xy,
ydata=my_np_array.ravel(),
p0=(400, 400,
3, 1,
5, 1)
)
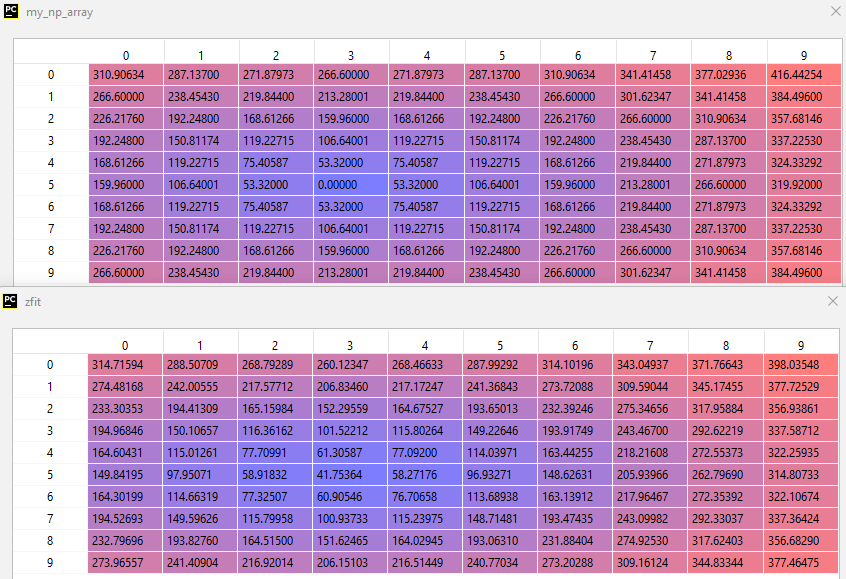
print(param)
zfit = gaussian2(xy, *param).reshape(my_np_array.shape)
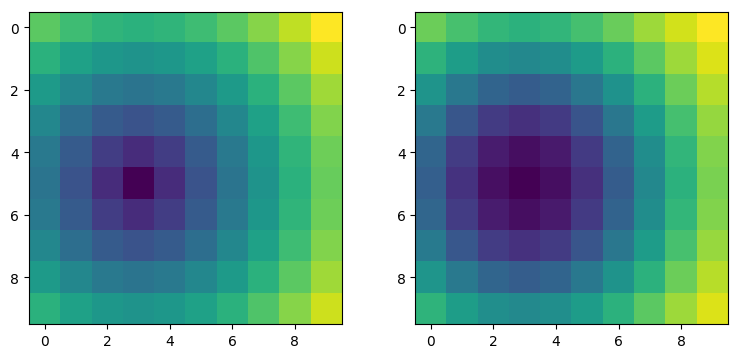
fig, (ax_act, ax_fit) = plt.subplots(nrows=1, ncols=2)
ax_act.imshow(my_np_array)
ax_fit.imshow(zfit)
plt.show()
[447.47305265 394.42329346 3.02857599 5.53214092 4.98984104
5.56048623]
It's too broad, so if you want a better fit you need to use something that isn't Gaussian. For instance, modified exponents of about 1.7 and 1.8 provide for an excellent fit - discounting your peak "0" which looks fake to me.
def gaussian2(xy: np.ndarray, a: float, b: float, c: float, d: float, e: float, f: float, g: float, h: float) -> np.ndarray:
x, y = xy
z = (
a - b
* np.exp(-np.abs((x - c)/d)**e)
* np.exp(-np.abs((y - f)/g)**h)
)
return z
param, _ = scipy.optimize.curve_fit(
f=gaussian2,
xdata=xy,
ydata=my_np_array.ravel(),
p0=(400, 400,
3, 5, 2,
5, 5, 2)
)
[482.96976151 441.22504655 3.01091214 6.11061124 1.79338408
5.00625763 6.27235212 1.69061652]
This will improve even further if you exclude the fake peak from the fit:
z_flat = my_np_array.ravel()
not_zero, = np.nonzero(z_flat)
z_flat = z_flat[not_zero]
xy = xy[:, not_zero]
# ...
zfit = np.zeros_like(my_np_array)
x, y = xy
zfit[y, x] = gaussian2(xy, *param)