Weird behavior in ggplot's stat_function()-CodePudding

I'm working with the dataset PatentsRD from the Ecdat library and came across a weird behavior with ggplot I have no explanaiton for.

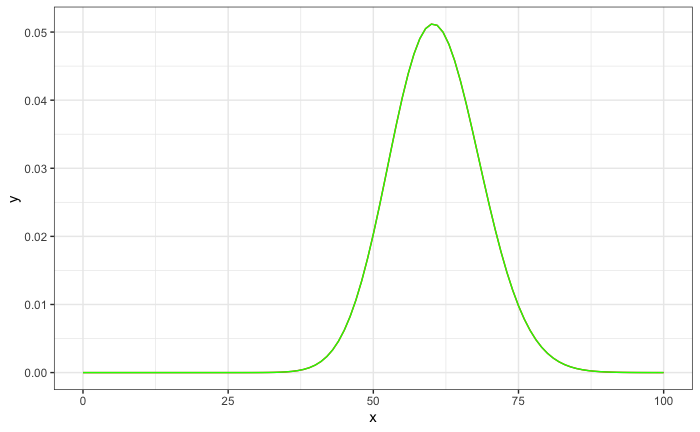
I plot two functions poisson distributions (once using the formula and once using dpois) to see wheter they are in fact identical:

library(tidyverse)
library(Ecdat)
data(PatentsRD)

plot <- ggplot(data = data.frame(x = c(0:100)), aes(x = x)) 
  stat_function(fun = function(x){(mean(PatentsRD$patent)^x)/(factorial(x))*exp(-mean(PatentsRD$patent))}, color = "red") 
  stat_function(fun = function(x){dpois(x, mean(PatentsRD$patent))}, color = "green")
plot

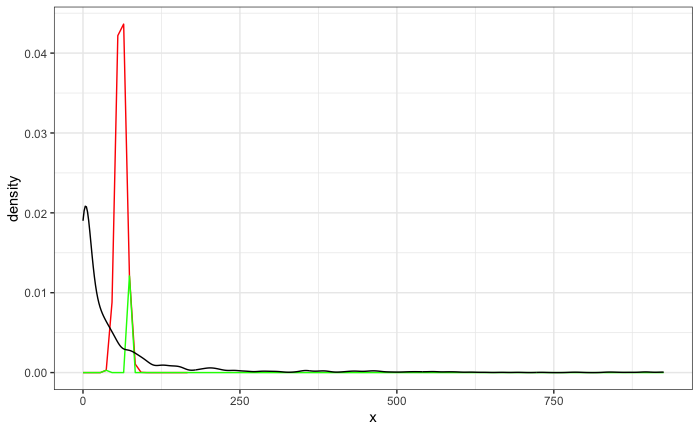
Great, both functions are exactly the same. But when I now try to add the density function of the data, things get messed up:

plot  
  geom_density(data = PatentsRD, aes(x = patent))

Why are the green and red function suddenly not equal to each other anymore? And neither green nor red have the right height (just above 0.05) anymore. Whats going on here?

CodePudding user response：

The issue here is that by default, stat_function calculates the y values at 101 points along the x axis. By coincidence, the data you have passed (x = 0:100), has exactly 101 evenly spaced elements. This means your functions are being evaluated at the integers on your initial plot.

When you add in the density plot, the x axis range increases dramatically to about 900 and therefore the resolution of the curves drops, since the curve will only be evaluated in 8.9 unit increments. For the red curve, this means that the function happens not to be calculated at the precise peak value (and it no longer looks smooth).

The situation is even worse with the green curve, since dpois returns 0 with non-integer values (along with a warning), so the green curve doesn't get evaluated properly at all. If you try making your first plot with x = 0:99 you will see the green curve is a flat line (zero everywhere).

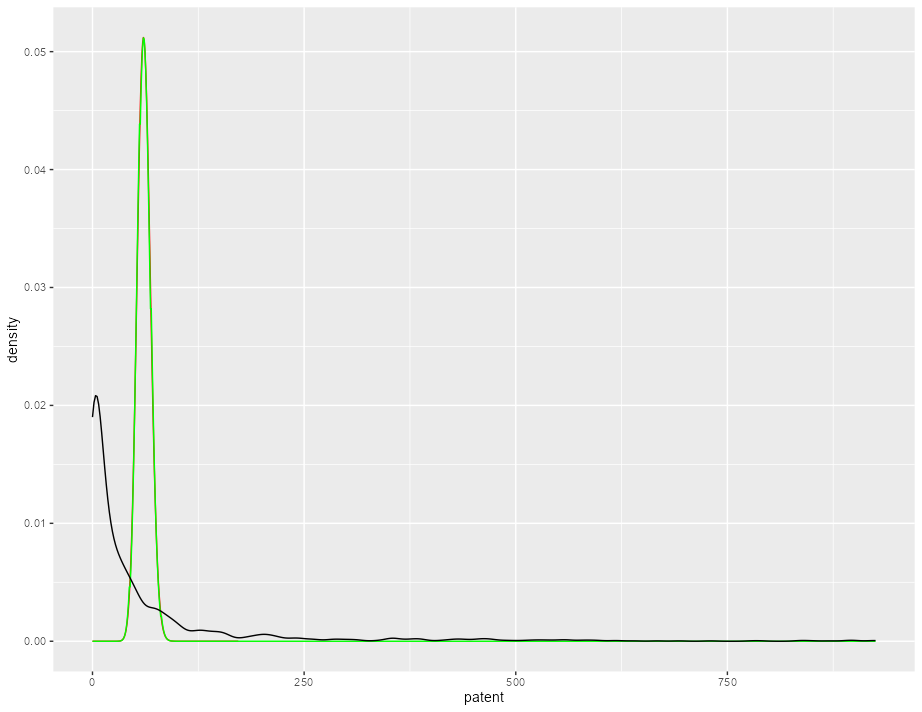
To fix the resolution issue, increase the n argument in stat_function, to say 1000.

To fix the green curve, evaluate at round(x) rather than x so that dpois always gives a value that applies to the nearest integer. (though one could argue that you shouldn't really represent a discrete distribution with a curve like this, since a series of vertical lines at the integer values is a more accurate depiction).

ggplot()  
  stat_function(fun = function(x){
    (mean(PatentsRD$patent)^x)/(factorial(x))*exp(-mean(PatentsRD$patent))
    }, color = "red", n = 1000) 
  stat_function(fun = function(x){dpois(round(x), mean(PatentsRD$patent))}, 
                color = "green", n = 1000)  
  geom_density(data = PatentsRD, aes(x = patent))