Good fitting a curve to the points in gnuplot or maybe in other program?-CodePudding

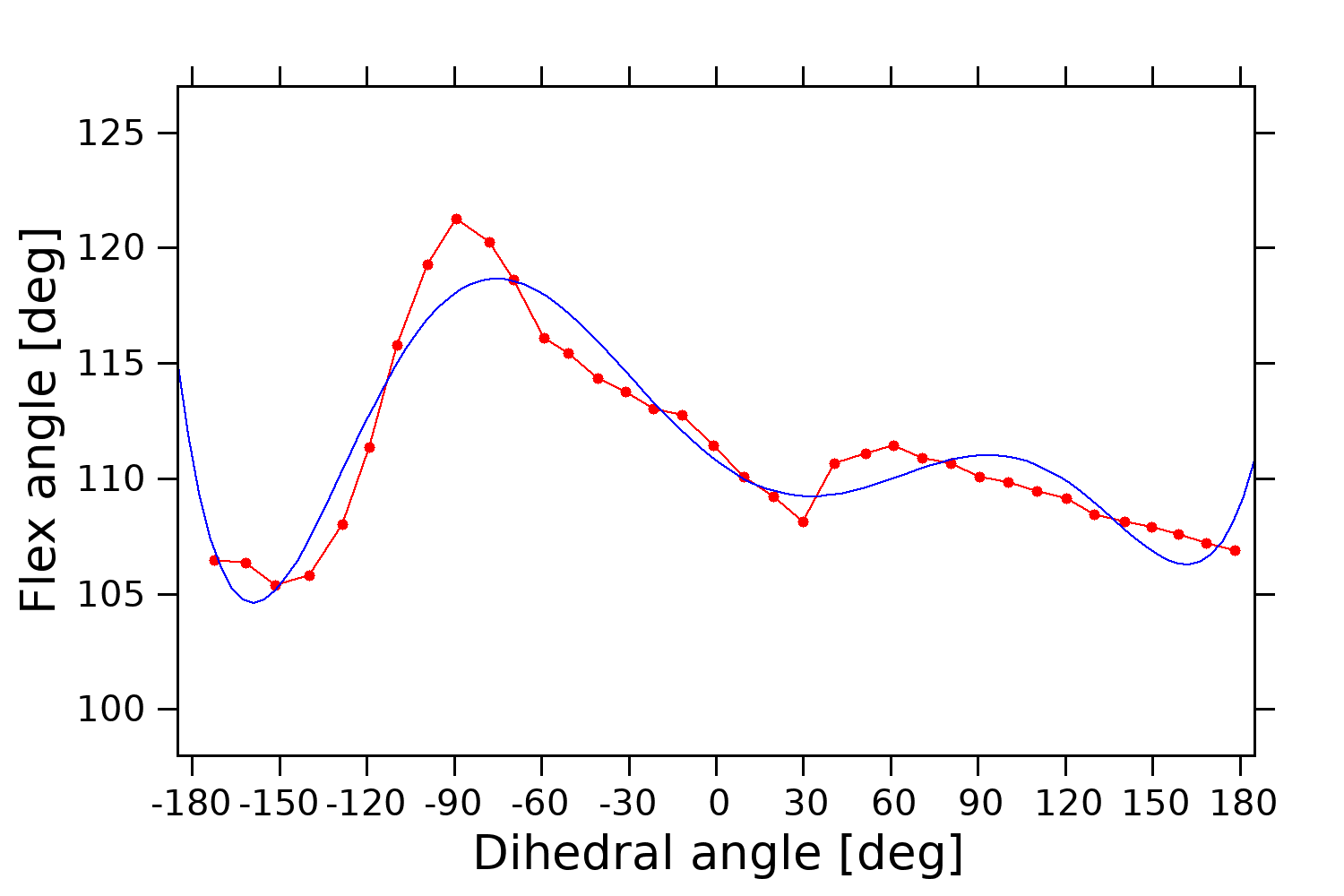
I have a huge problem. I want to have the best fitting curve through these points very well. In gnuplot I try this.

f(x) = a*x**6   b*x**5   c*x**4   d*x**3   e*x**2   f*x   g
fit f(x) 'dihedral_energy_sorted.txt' via a, b, c, d, e, f, g
plot 'dihedral_energy_sorted.txt' with points pointtype 7 pointsize 2 linecolor "red", 'dihedral_energy_sorted.txt' with lines lw 2 linecolor "red", f(x) with lines lw 2 linecolor "blue"

But my results are not so good.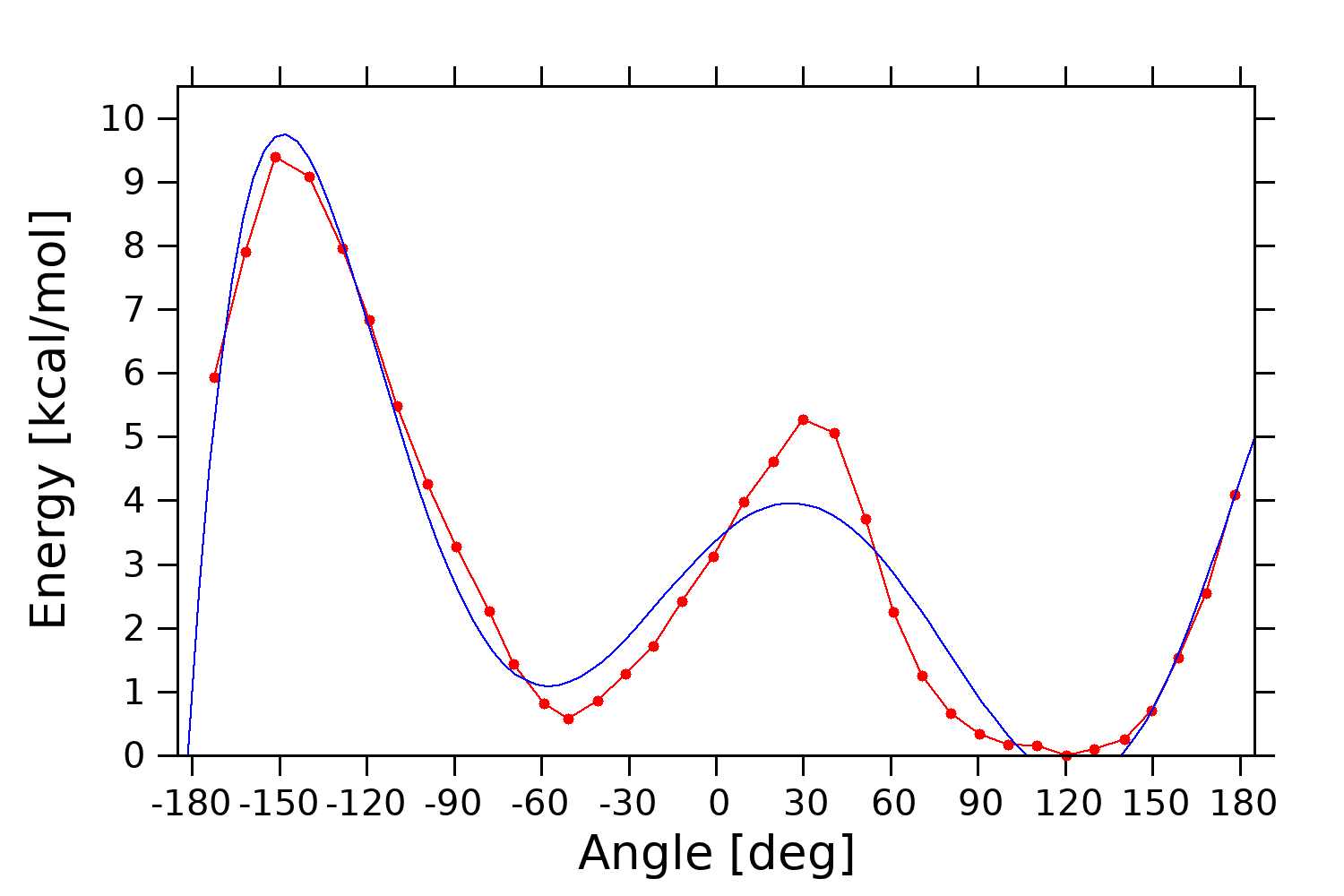

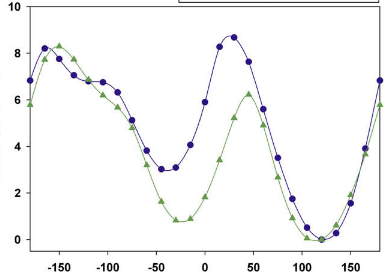
I need something much better, which gives me a line graph that goes through the points and is much more smooth not just points connected by lines.

Maybe in excel or matplotlib I have something which could help me

I need fit something like that

This is data from the first file

-172.266    5.93362
-161.743    7.90223
-151.444    9.39198
-139.667    9.07427
-128.472    7.94997
-118.986    6.82431
-109.593    5.48811
-99.149 4.25969
-89.297 3.26822
-78.018 2.26675
-69.572 1.43405
-59.157 0.814157
-50.830 0.57777
-40.542 0.859919
-30.995 1.28429
-21.507 1.70913
-11.557 2.41328
-0.911  3.12653
9.526   3.97824
19.606  4.61242
29.856  5.27657
40.725  5.0631
51.336  3.71232
61.068  2.25515
70.685  1.25386
80.499  0.655369
90.433  0.332484
100.257 0.167369
110.170 0.156063
120.393 0
129.920 0.100962
140.245 0.258918
149.617 0.698804
158.873 1.52595
168.424 2.53915
178.232 4.08872

This is data from the second file

-172.266    106.470
-161.743    106.362
-151.444    105.361
-139.667    105.809
-128.472    108.023
-118.986    111.368
-109.593    115.765
-99.149 119.263
-89.297 121.257
-78.018 120.227
-69.572 118.617
-59.157 116.109
-50.830 115.423
-40.542 114.353
-30.995 113.756
-21.507 113.016
-11.557 112.750
-0.911  111.413
9.526   110.081
19.606  109.232
29.856  108.139
40.725  110.666
51.336  111.101
61.068  111.435
70.685  110.908
80.499  110.659
90.433  110.070
100.257 109.833
110.170 109.453
120.393 109.125
129.920 108.426
140.245 108.150
149.617 107.904
158.873 107.596
168.424 107.216
178.232 106.899

CodePudding user response：

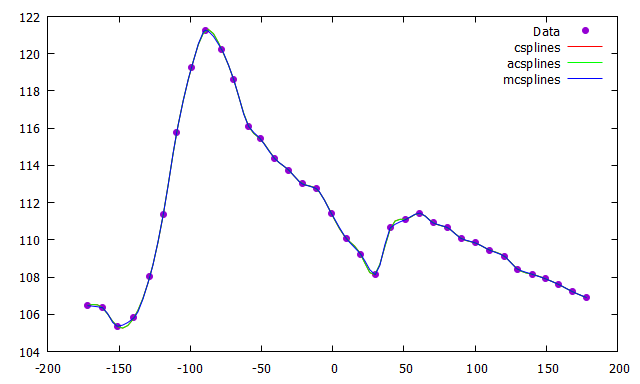
According to the SO-"rule", no answers in comments: Here is an answer. Check help smooth and one of the splines options. With this large number of points the different splines options do not differ that much.

Code:

### smooth slpines
reset session

$Data <<EOD
-172.266    106.470
-161.743    106.362
-151.444    105.361
-139.667    105.809
-128.472    108.023
-118.986    111.368
-109.593    115.765
-99.149 119.263
-89.297 121.257
-78.018 120.227
-69.572 118.617
-59.157 116.109
-50.830 115.423
-40.542 114.353
-30.995 113.756
-21.507 113.016
-11.557 112.750
-0.911  111.413
9.526   110.081
19.606  109.232
29.856  108.139
40.725  110.666
51.336  111.101
61.068  111.435
70.685  110.908
80.499  110.659
90.433  110.070
100.257 109.833
110.170 109.453
120.393 109.125
129.920 108.426
140.245 108.150
149.617 107.904
158.873 107.596
168.424 107.216
178.232 106.899
EOD

plot $Data u 1:2 w p pt 7                    ti "Data", \
        '' u 1:2 smooth csplines  lc "red"   ti "csplines", \
        '' u 1:2 smooth acsplines lc "green" ti "acsplines", \
        '' u 1:2 smooth mcsplines lc "blue"  ti "mcsplines"
### end of code

Result: