This question was
CodePudding user response:
- Use
np.linspace to create an array for the x values. Use many points to create the circle
- Use
np.sqrt to solve for an array, instead of looping through each value.
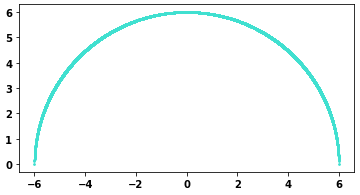
import numpy as np
import matplotlib.pyplot as plt
def semicircle(r, h, k):
x0 = h - r
x1 = h r
x = np.linspace(x0, x1, 10000)
y = k np.sqrt(r**2 - (x - h)**2)
return x, y
x, y = semicircle(6, 0, 0)
plt.scatter(x, y, s=3, c='turquoise')
plt.gca().set_aspect('equal', adjustable='box')
CodePudding user response:
Answering my own question.
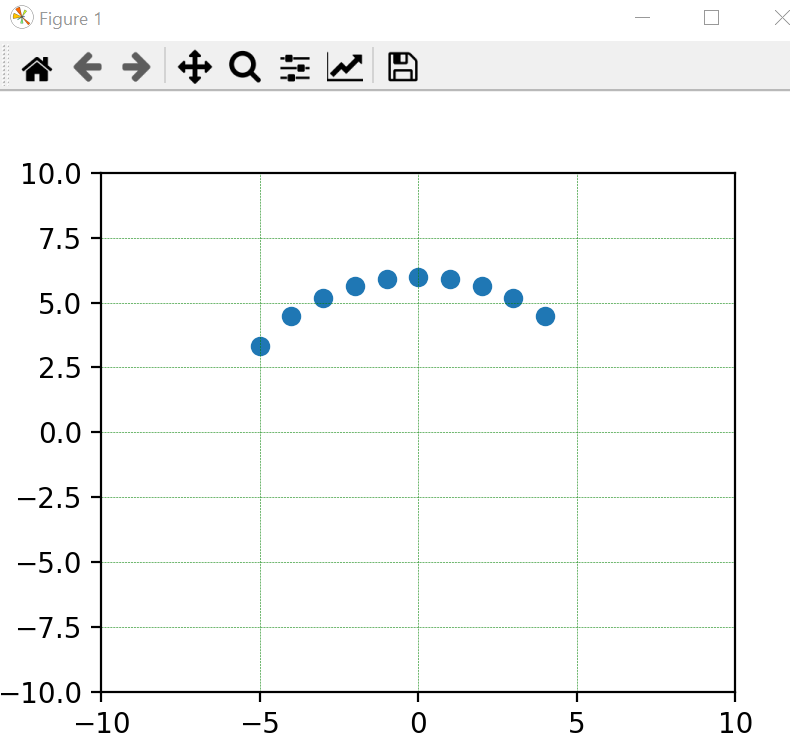
Plotting the output of the code:
import math
import numpy as np
import matplotlib.pyplot as plt
coord_list = []
h = 0
k = 0
r = 6
for x in range((1 h - r), (h r - 1), 1):
y1 = k math.sqrt(r**2 - (x-h)**2)
coord_list.append([x, y1])
for each in coord_list:
print(each)
data = np.array([coord_list])
x, y = data.T
figure = plt.scatter(x, y)
figure = plt.grid(color = 'green', linestyle = '--', linewidth = 0.2)
figure = plt.show()
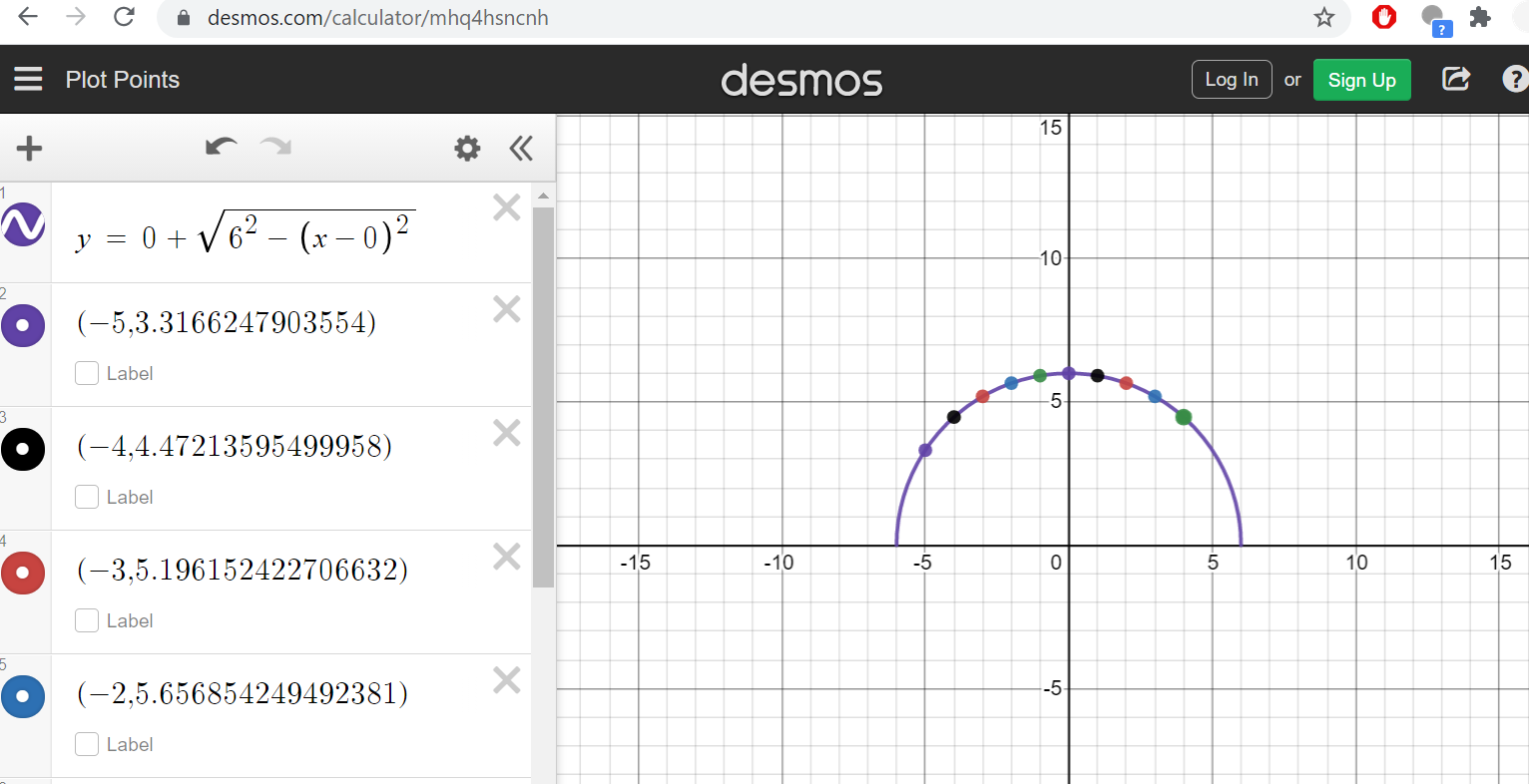
[-5, 3.3166247903554]
[-4, 4.47213595499958]
[-3, 5.196152422706632]
[-2, 5.656854249492381]
[-1, 5.916079783099616]
[0, 6.0]
[1, 5.916079783099616]
[2, 5.656854249492381]
[3, 5.196152422706632]
[4, 4.47213595499958]
Looking at the output of the coordinates, it doesn't appear to be a circle.
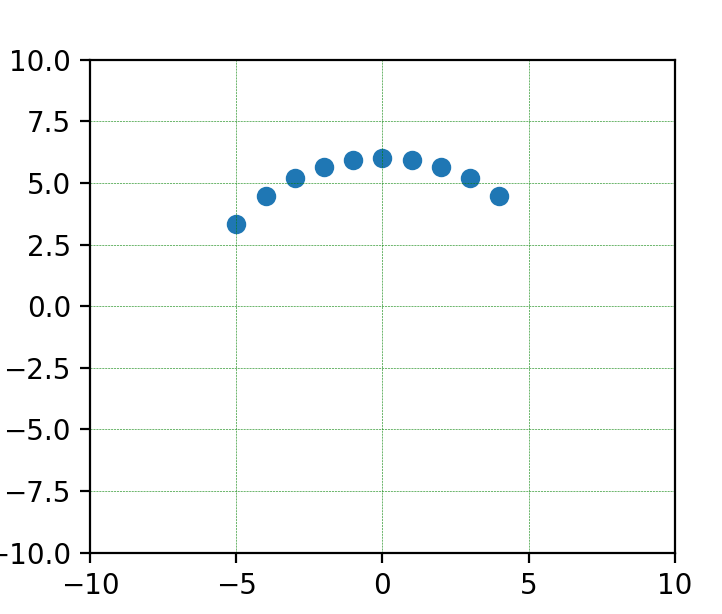
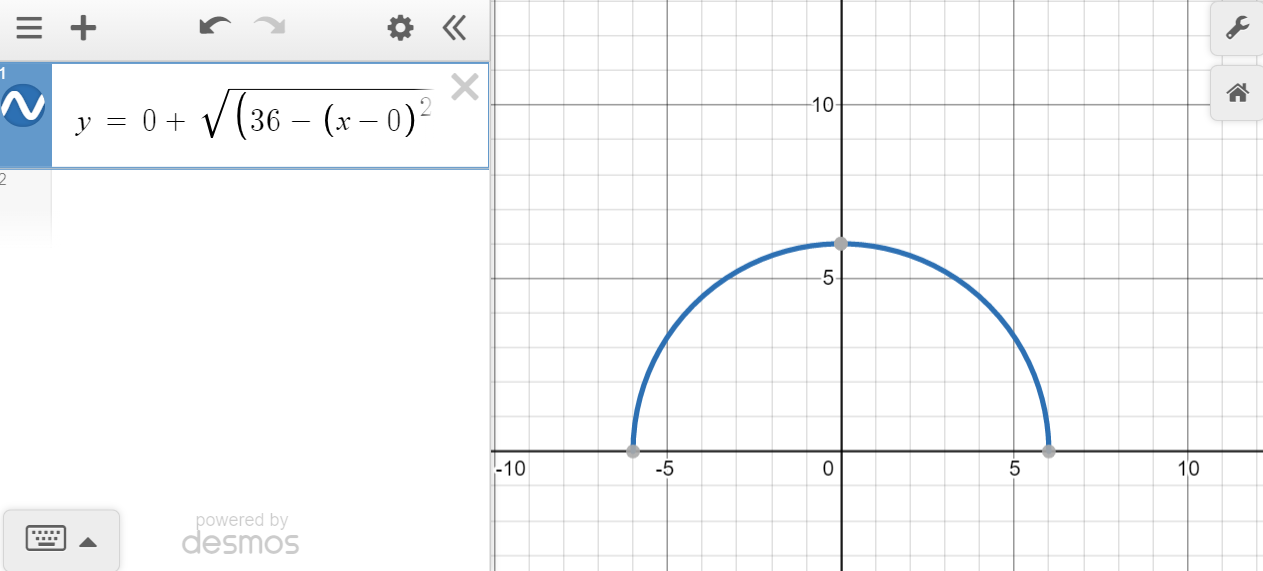
But if we take our equation and our coordinates and graph them on this website we see that they are indeed a circle. It's an optical illusion that they aren't. Partially because the graph is not evenly displayed and also because plotting points in a range function with steps of 1 (line 13) doesn't plot points at equal arc length distances away from each other.