I am reading about numpy's reshape method. Here is the quote:

Note that for this (i.e. reshaping) to work, the size of the initial array must match the size of the reshaped array. Where possible, the reshape method will use a no-copy view of the initial array, but with noncontiguous memory buffers this is not always the case.

I did a few simple tests and it seems reshape indeed does not create a copy, the memory is shared.

So what does that part here mean "but with noncontiguous memory buffers this is not always the case"? What is an example where reshape does create a copy of the data? And what are the rules really i.e. when exactly does it create a copy and when not?

CodePudding user response：

Example of a view vs copy

Here is an example of a copy being created for a reshape operation. We can check if two arrays share memory or not with np.share_memory. If True then one of them is a view of the other and if False then one of them is a copy of the other and is stored in a separate memory. Meaning, any operations on one don't reflect on the other.

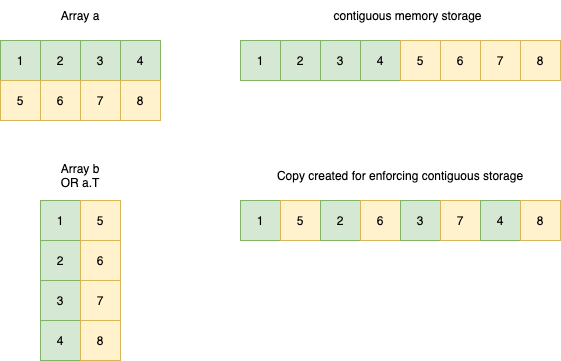
a = np.array([[1,2,3,4],[5,6,7,8]])
b = a.T

arr1 = a.reshape((-1,1))
print('Reshape of original is a view:', np.shares_memory(a, arr1))

print('Transpose sharing memory:', np.shares_memory(a,b))

arr2 = b.reshape((-1,1))
print('Reshape of transpose is a view:', np.shares_memory(b, arr2))

Reshape of original is a view: True    #<- a, a.reshape share memory
Transpose sharing memory: True         #<- a, a.T share memory
Reshape of transpose is a view: False  #<- a.T, a.T.reshape DONT share memory

EXPLANATION:

How numpy stores arrays?

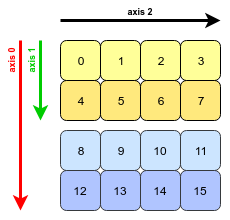
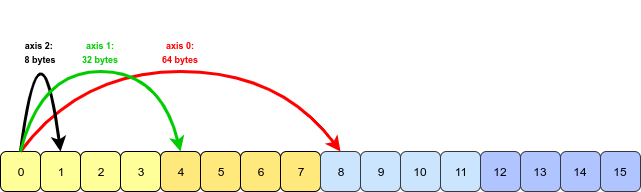
Numpy stores its ndarrays as contiguous blocks of memory. Each element is stored in a sequential manner every n bytes after the previous.

(images referenced from this

Then in memory its stores as -

When retrieving an element (or a block of elements), NumPy calculates how many strides (of 8 bytes each) it needs to traverse to get the next element in that direction/axis. So, for the above example, for axis=2 it has to traverse 8 bytes (depending on the datatype) but for axis=1 it has to traverse 8*4 bytes, and axis=0 it needs 8*8 bytes.

Almost all numpy operations depend on this nature of storage of the arrays. So, to work with an array that can comprise of non-contiguous blocks of memory, numpy is sometimes forced to create copies instead of views.

Why reshape may create a copy sometimes?

Coming back to the example that I show above with array a and a.T, let's look at the first example. We have an array a which is stored as a contiguous block of memory as below -

Since an array needs to be stored in a contiguous manner so that other numpy operations can be properly applied, it is forced to create a copy of the numpy array since its really difficult to keep a track of the memory associated with the original elements for subsequent operations. This is why the a.T gets a reshape output as a copy in this case.

Hopefully, this should explain your query. I am not that great at articulating so do let me know what part is confusing to you and I can edit my answer for a clearer explanation.

CodePudding user response：

I was going to repeat the core of my linked answer, and say that transpose is the most likely case where reshape will produce a copy.

But then I thought of a case where the view is produces a non-contiguous selection:

In [181]: x = np.arange(16).reshape(4,4)
In [182]: x1 = x[::2,::2]
In [183]: x
Out[183]: 
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])
In [184]: x1
Out[184]: 
array([[ 0,  2],
       [ 8, 10]])
In [185]: x1[0,0]=100
In [186]: x
Out[186]: 
array([[100,   1,   2,   3],
       [  4,   5,   6,   7],
       [  8,   9,  10,  11],
       [ 12,  13,  14,  15]])

x1, created with basic indexing, is a view. But a reshape of it is a copy:

In [187]: x2 = x1.reshape(-1)
In [188]: x2
Out[188]: array([100,   2,   8,  10])
In [189]: x2[0] = 200
In [190]: x1
Out[190]: 
array([[100,   2],
       [  8,  10]])
In [191]: x
Out[191]: 
array([[100,   1,   2,   3],
       [  4,   5,   6,   7],
       [  8,   9,  10,  11],
       [ 12,  13,  14,  15]])

A simple test for a copy is to look at the ravel. ravel is a reshape; if the ravel isn't the same as the originals, or a subset of it, it's a copy.

In [192]: x.ravel()
Out[192]: 
array([100,   1,   2,   3,   4,   5,   6,   7,   8,   9,  10,  11,  12,
        13,  14,  15])
In [193]: x1.ravel()
Out[193]: array([100,   2,   8,  10])    # x1 is a view, but a reshape is a copy
In [194]: xt = x.T
In [195]: xt
Out[195]: 
array([[100,   4,   8,  12],
       [  1,   5,   9,  13],
       [  2,   6,  10,  14],
       [  3,   7,  11,  15]])
In [196]: xt.ravel()   # xt is a view, but its reshape is a copy
Out[196]: 
array([100,   4,   8,  12,   1,   5,   9,  13,   2,   6,  10,  14,   3,
         7,  11,  15])

selecting two rows is a view, and its reshape is one too:

In [197]: x[:2].ravel()
Out[197]: array([100,   1,   2,   3,   4,   5,   6,   7])
In [198]: x[:2].ravel()[0]=200
In [199]: x
Out[199]: 
array([[200,   1,   2,   3],
       [  4,   5,   6,   7],
       [  8,   9,  10,  11],
       [ 12,  13,  14,  15]])

but not when selecting two columns:

In [200]: x[:,:2].ravel()
Out[200]: array([200,   1,   4,   5,   8,   9,  12,  13])
In [201]: x[:,:2].ravel()[0]=150
In [202]: x
Out[202]: 
array([[200,   1,   2,   3],
       [  4,   5,   6,   7],
       [  8,   9,  10,  11],
       [ 12,  13,  14,  15]])

As for predicting a copy without actually doing it - I'd depend more on experience than some code (which I attempted in the linked answer). I have a good idea of how the data is layed out, or can easily test for it.

Keep in mind when this copy/no-copy is important. As I showed, the copy case keeps us from modifying the original array. Whether that's good or not depends on the situation. In other cases we don't really care. The performance cost of a copy isn't that great.