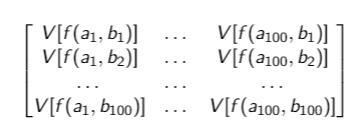Numpy - How pass from 3d matrix in 2d with this algorithm-CodePudding

I need to have a more efficient code, that the one implemented by me below. Is it possible to have a more efficient code, also using numpy?

I am going to explain my algorithm and how it works. Considering the figure below, I have a matrix that contains 10000 matrix inside, and each matrix inside has a dimension 100x100.

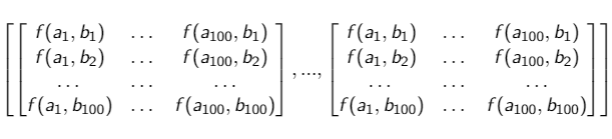
My output should be a matrix 100x100, like this:

therefore, the first element of my "output" V[f(a_1,b_1)] is the variance of all f(a_1,b_1) elements contained in 10000 matrices. Thus, I need to compute the variances of the elements with the same index.

Below there is the code used, it should be correct (I hope..). is it possible to have a more efficient code? (for simplicity, I simulate the input with random numbers, since the matrix is too big to post here)

import numpy as np
input = np.random.randint(0, 100, size=(10000, 100, 100))
output = []
for n in range(100):
    row = []
    for i in range(100):
        row2 = [] 
        for m in range(10000):
            P_mi_sigmai = input[m][n][i]
            row2.append(P_mi_sigmai)
        variance = np.var(row2) 
        row.append(variance)
    output.append(row)
print(np.array(output).shape)

CodePudding user response：

Here's how i would do it:

output = input.var(axis = 0)

Here's a minimal reprex:

import numpy as np

arr = np.random.rand(5, 2, 2)
arr[:, 0, 0] = 1
var_arr = arr.var(0)


print(f'arr = \n{arr}')
print(f'var_arr = \n{var_arr}')

output:

arr = 
[[[1.         0.13682225]
  [0.24076008 0.61107865]]

 [[1.         0.99948733]
  [0.61871626 0.64518322]]

 [[1.         0.7979549 ]
  [0.53991881 0.17229415]]

 [[1.         0.13547922]
  [0.97390205 0.50778721]]

 [[1.         0.74116566]
  [0.05428085 0.86287107]]]
var_arr = 
[[0.         0.12837323]
 [0.10101842 0.05092759]]

I'm not gonna show it here, but using your code i get the same result