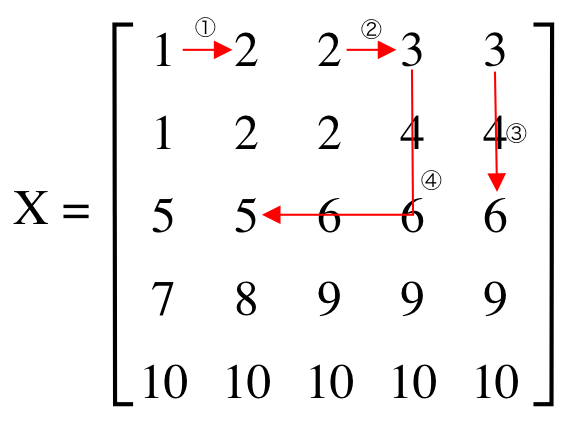
I am trying to find the minimum number of hops to get from the value of one cell w to the value of another cell v in the following matrix X using Python.
Is there an efficient way to do this?
import numpy as np
from numpy.typing import NDArray
def manhattan_distance(X: NDArray[int], w: int, v: int) -> int:
# something
return distance
X = np.array([
[1, 2, 2, 3, 3],
[1, 2, 2, 4, 4],
[5, 5, 6, 6, 6],
[7, 8, 9, 9, 9],
[10, 10, 10, 10, 10],
]).astype(np.int_)
# Expected result
manhattan_distance(X, 1, 2) # ①
-> 1
manhattan_distance(X, 2, 3) # ②
-> 1
manhattan_distance(X, 3, 6) # ③
-> 2
manhattan_distance(X, 3, 5) # ④
-> 4
I tried to implement it as follows, but it seems to be quite slow.
import numpy as np
from numpy.typing import NDArray
def manhattan_distance(X: NDArray[int], w: int, v: int) -> int:
xx, yy = np.where(X == w)
xx_, yy_ = np.where(X == v)
distance = int(min_dist(xx, xx_) min_dist(yy, yy_))
return distance
def min_dist(xx, xx_):
min_dist = np.inf
for i in xx:
for j in xx_:
dist = np.sqrt((i - j)**2)
min_dist = dist if dist < min_dist else min_dist
return min_dist
Is there any way to speed this calculation up?
CodePudding user response:
Use cdist to compute all pairwise distances, to find the values' indices use np.argwhere
from scipy.spatial.distance import cdist
import numpy as np
from numpy.typing import NDArray
X = np.array([
[1, 2, 2, 3, 3],
[1, 2, 2, 4, 4],
[5, 5, 6, 6, 6],
[7, 8, 9, 9, 9],
[10, 10, 10, 10, 10],
]).astype(np.int32)
def manhattan_distance(X: NDArray[int], w: int, v: int) -> int:
return cdist(np.argwhere(X == w), np.argwhere(X == v), "cityblock").min()
print(manhattan_distance(X, 1, 2))
print(manhattan_distance(X, 2, 3))
print(manhattan_distance(X, 3, 6))
print(manhattan_distance(X, 3, 5))
Output
1.0
1.0
2.0
4.0
CodePudding user response:
Just adding timings for different matrix sizes to show OP that @Dani Mesejo answer indeed is much faster. For small matrices differences will be small of course.
def manhattan_distance_dani_masejo(X, w: int, v: int) -> int:
return cdist(np.argwhere(X == w), np.argwhere(X == v), "cityblock").min()
def manhattan_distance_ugen(X, w: int, v: int) -> int:
xx, yy = np.where(X == w)
xx_, yy_ = np.where(X == v)
distance = int(min_dist(xx, xx_) min_dist(yy, yy_))
return distance
def min_dist(xx, xx_):
min_dist = np.inf
for i in xx:
for j in xx_:
dist = np.sqrt((i - j)**2)
min_dist = dist if dist < min_dist else min_dist
return min_dist
def gen_data(matrix_size):
return np.random.randint(0, matrix_size, (matrix_size, matrix_size), dtype=np.int32)
for matrix_size in [5, 50, 500]:
print('Matrix size: {}'.format(matrix_size))
X = gen_data(matrix_size)
print('ugen: ', timeit.timeit("manhattan_distance_ugen(X, np.random.randint(0, matrix_size), np.random.randint(0, matrix_size))",
"from __main__ import manhattan_distance_ugen, X, matrix_size; import numpy as np",
number=10))
print('dani masejo: ', timeit.timeit("manhattan_distance_dani_masejo(X, np.random.randint(0, matrix_size), np.random.randint(0, matrix_size))",
"from __main__ import manhattan_distance_dani_masejo, X, matrix_size; import numpy as np",
number=10))
Result:
Matrix size: 5
ugen: 0.0019634239999999914
dani masejo: 0.0006071939999999776
Matrix size: 50
ugen: 0.093326557
dani masejo: 0.0008874660000000034
Matrix size: 500
ugen: 9.112327058
dani masejo: 0.027754558000001595