Solve complex equations in R-CodePudding

I have an equation like where a, b, c and d are constants :

(b/(4.2410^-11))(1-2*x) log(x/(1-x)) - log((a/(1-a))*c/d)) = 0

How can I solve this equation in R for finding x?

CodePudding user response：

1) Assuming that the constants all equal 0.1 and that the value of x which solves the equation lies between 0.1 and .9 we have:

f <- function(x, a, b, c, d) (b/(4.2410^-11))*(1-2*x)   
  log(x/(1-x)) - log((a/(1-a))*c/d)
uniroot(f, c(0.1, 0.9), a = .1, b = .1, c = .1, d = .1)
str(ans)

giving:

List of 5
 $ root      : num 0.5
 $ f.root    : num -8.54e-07
 $ iter      : int 2
 $ init.it   : int NA
 $ estim.prec: num 6.1e-05

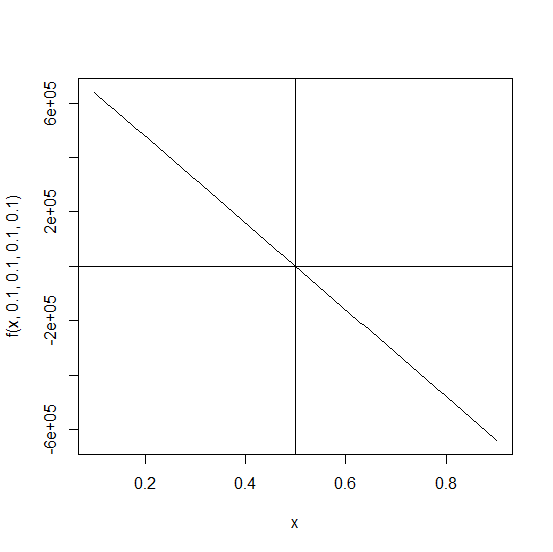
We can graph it like this:

curve(f(x, .1, .1, .1, .1), 0.1, 0.9)
abline(v = ans$root, h = ans$f.root)

2) Another possibility is to rearrange the equation to give:

x = ( 1 (log(x/(1-x)) - log((a/(1-a))*c/d)) / (b/(4.2410^-11)))/2

and then iterate that. Note that it immediately converged.

a <- b <- c <- d <- 0.1
x <- 0.25
for(i in 1:10) print(
    x <- ( 1 (log(x/(1-x)) - log((a/(1-a))*c/d)) / (b/(4.2410^-11)))/2
  )

giving:

[1] 0.5000007
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014
[1] 0.5000014