Coefficient matrix and loops challenge-CodePudding

I'm trying to solve the equation for T(p,q) as shown more clearly in the attached image.

Where:

p = 0.60
q = 0.45
M - coefficient matrix with 3 rows and 6 columns

I created five matrices and put them within their own functions in order to later call them in the while loop. However, the loop doesn't cycle through the various values of i.

How can I get the loop to work or is there another/better way I can solve the following equation?

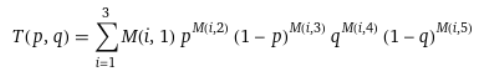
the equation I'm trying to solve

(FYI this is approx my third day ever working with Python and coding)

import numpy as np

def M1(i):
    M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
    return M[i-1,0]

def M2(i):
    M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
    return M[i-1,1]

def M3(i):
    M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
    return M[i-1,2]

def M4(i):
    M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
    return M[i-1,3]

def M5(i):
    M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
    return M[i-1,4]

def T(p,q):
    sum_i = 0
    i = 1
    while i <=5:
        sum_i = sum_i   ((M1(i)*p**M2(i))*((1-p)**M3(i))*(q**M4(i))*((1-q)**M5(i)))
        i = i  1
        return sum_i

print(T(0.6,0.45))

"""I printed the below equation (using a single value for i) to test if the above loop is working and since I get the same answer as the loop, I can see that the loop is not cycling through the various values of i as expected"""

i=1
p=0.6
q=0.45
print(((M1(i)*p**M2(i))*((1-p)**M3(i))*(q**M4(i))*((1-q)**M5(i))))

CodePudding user response：

return is placed inside while loop, you need to change the code a bit

    while i <=5:
        sum_i = sum_i   ((M1(i)*p**M2(i))*((1-p)**M3(i))*(q**M4(i))*((1-q)**M5(i)))
        i = i  1
    return sum_i

CodePudding user response：

The real power with numpy is to look at computations like these and try to understand what is repeatable and what structure they have. Once you find operations that are similar or parallel, try to set up your numpy function calls so that they can be done element-wise in parallel with one call.

For instance, inside the typical element of the sum, there are four things being explicitly raised to a power (a fifth if you consider M(i, 1)^1). In one function call, you can perform all four of these exponentiations in parallel with one function call if you arrange your arrays smartly:

M = np.array([[1,3,0,4,0,0],[3,3,1,4,0,0],[4,4,0,3,1,0]])
ps_and_qs = np.array([[p, (1-p), q, (1-q)]])

a = np.power(ps_and_qs, M[:,1:5])

Now a will be populated with a 3 x 4 matrix with all of your exponentiations.

Now the next step is how to reduce these. There are several reduction functions that are built into numpy that are efficiently implemented with vectorized loops where possible. They can speed up your code quite a bit. In particular, there is both a product reduction as well as a sum reduction. With your equation, we need to first multiply across the rows to get one number per row and then sum across the remaining column like this:

b = M[:,:1] * np.product(a,axis=1)
c = np.sum(b, axis=0)

c should now be a scalar equal to T evaluated at (p,q). That is a lot to take in for a third day, but something to consider if you continue to use numpy for numerical analysis on bigger projects that need better performance.