I have an undirected and connected (not complete) graph of vertices, where u and v can be any 2 distinct vertices. I want to construct the minimum weight circuit that starts from a vertex u, passes through v, then returns back to u without repeating any edges. Can this be done by doing the following?

1. Finding the shortest path from u to v - call this p1

2. Removing all constituent edges of p1 from the graph

3. Finding the new shortest path from v to u - call this p2

4. Returning all deleted edges to the graph, and concatenating p1 and p2 together - call this c1

Is c1 the minimum weight circuit that can be constructed, considering the constraint of passing through both u and v? If so, how can I prove it, if not, why not?

It seems to make sense to me, as all the paths contained within c1 are also shortest paths themselves, however I can't quite shake the feeling that I might be missing something.

EDIT: I have changed "fully connected graph" to "connected graph". "fully" implied that the graph is complete, which is not what I meant.

CodePudding user response：

Here is a counterexample:

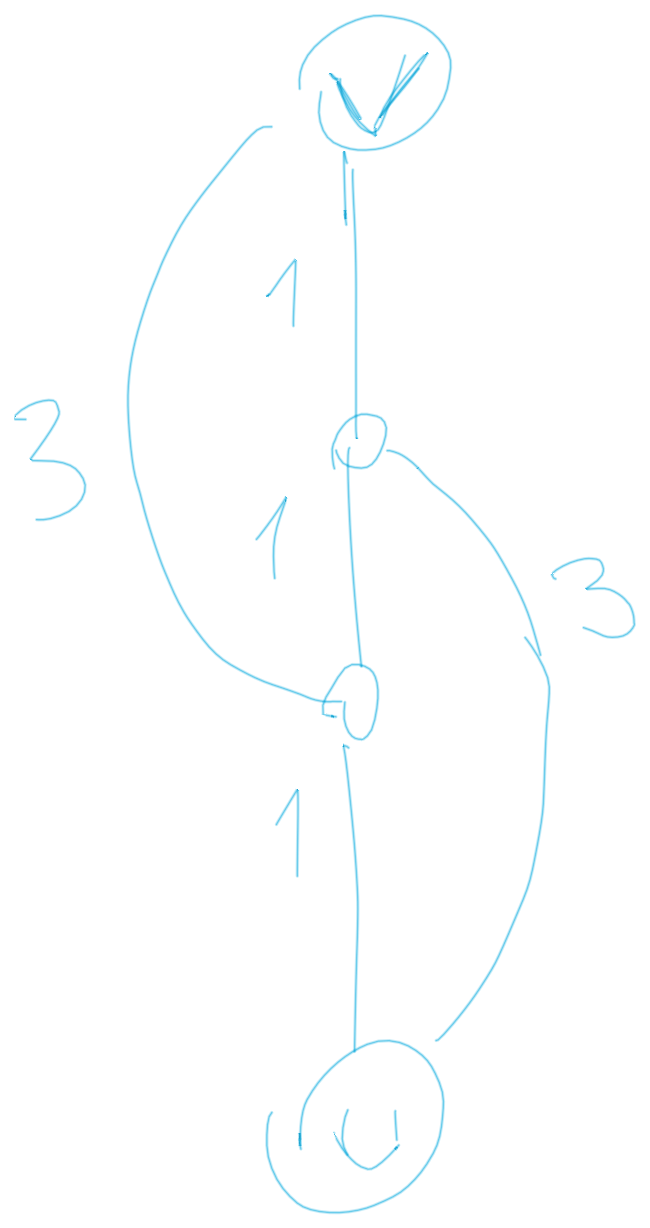
In a case of complete graph, assume all edges not shown in the picture to have some large weight (like 1000).

The p1 would find the shortest path 1 - 1 - 1 and exclude it, prohibiting the actual answer of 3 - 1 1 - 3.

I think your task is a variant of the Vehicle Routing Problem, which is the generalization of the Traveling Salesman Problem and it is NP-hard.

Meaning, to solve your problem, you have to consider all paths between u and v and for each such path find the shortest path back, avoiding using same edges.