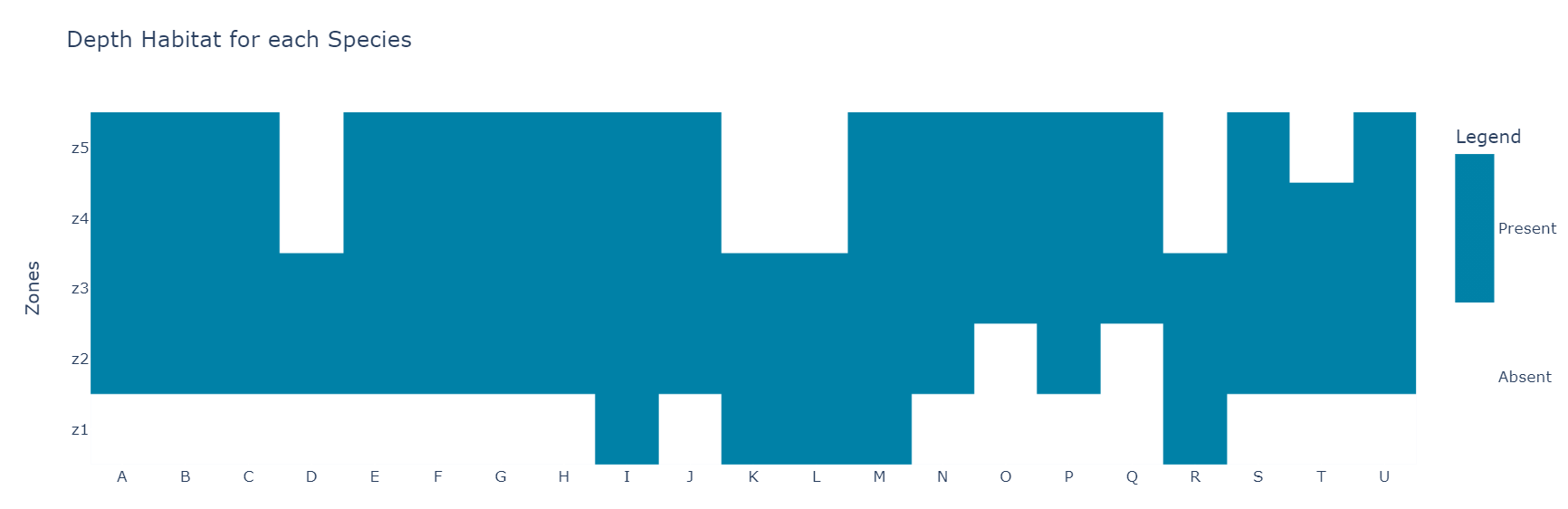
The data I'm working on represent the presence or the absence of some species in 5 habitats. I want to obtain clusters according to the shared zones between them, basically i want to maximize the matches between elements for each species.
This is the original dataset

And this is the type of sorting I'm looking for
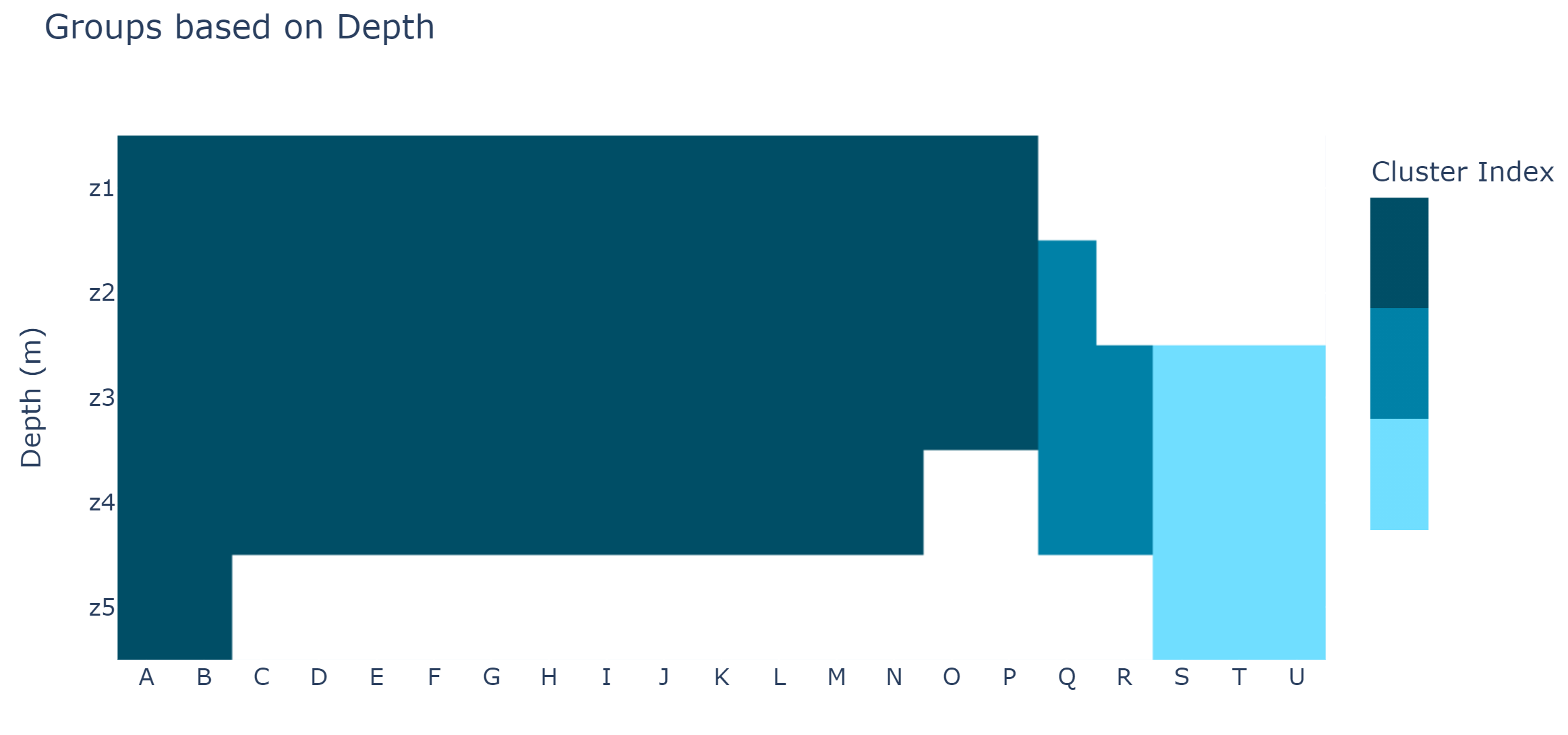
I managed to obtain 3 groups by simply sorting on the numbers of occupied zones and then manually fixing evident errors.
This very simplified algorithm only worked because occupied zones are always contiguous, and some common pattern are present.

At first I thought this problem was somewhat similar to

CodePudding user response：

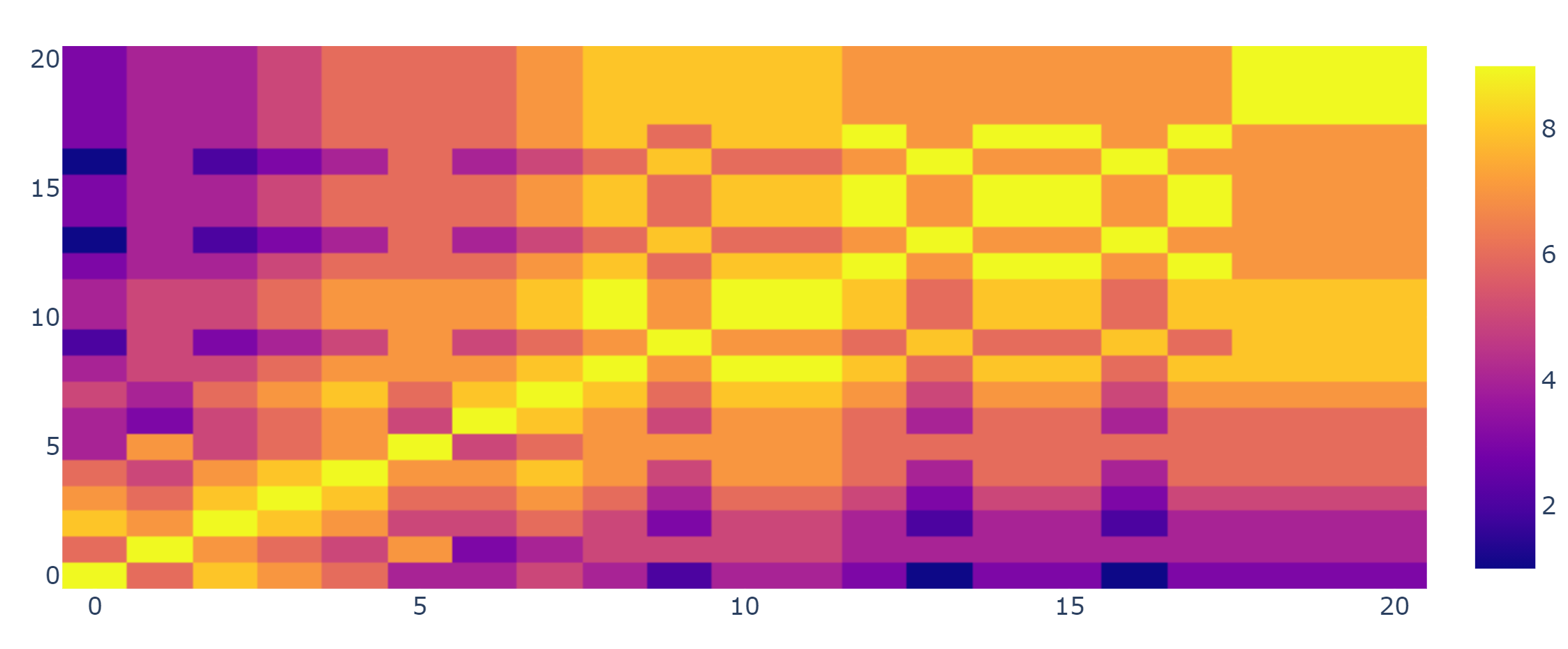
I think I solved this problem in a simple yet appropriate way (I'm sure there may be better algorithms though). I check the number of matches between each couple of boolean vectors:

n=len(diet_bool_df['Prey'])
match_mtx = [[0 for i in range(n)] for j in range(n)] #empty matrix nxn

for i in range(n):
    for j in range(n):
#this gives a vector containing 1 for a match and 0 for a mismatch position-wise
        match_vec = [int(diet_bool_df['Boolean Diet'][i][k]==diet_bool_df['Prey'][j][k]) for k in range(len(diet_bool_df['Prey'][i]))]
#the sum of all 1 gives the number of matches between each couple (i,j)
        match_mtx[i][j] = sum(match_vec)

Since there are 9 preys there will be a maximum of 9 matches, which will indicate identical diets. This new matrix now can be actually clusterized with kmeans because data are isotropic and all assumptions should be met.

def plot_match_cluster():
    fig= go.Figure()
    fig.add_trace(go.Heatmap(
        z=match_mtx,
    ))
    fig.show()

kmeans = sklearn.cluster.KMeans(n_clusters=3).fit_predict(match_mtx)

The new clusterized data looks like this
Clusterized Data

NB. Interestingly enough the initial sorting I decided according to the number of preys is a good indicator in this scenario to create clusters. This is only true with 3 clusters though.