Sierpinksi Triangle using Chaos Game - Incorrect Plot (missing points)-CodePudding

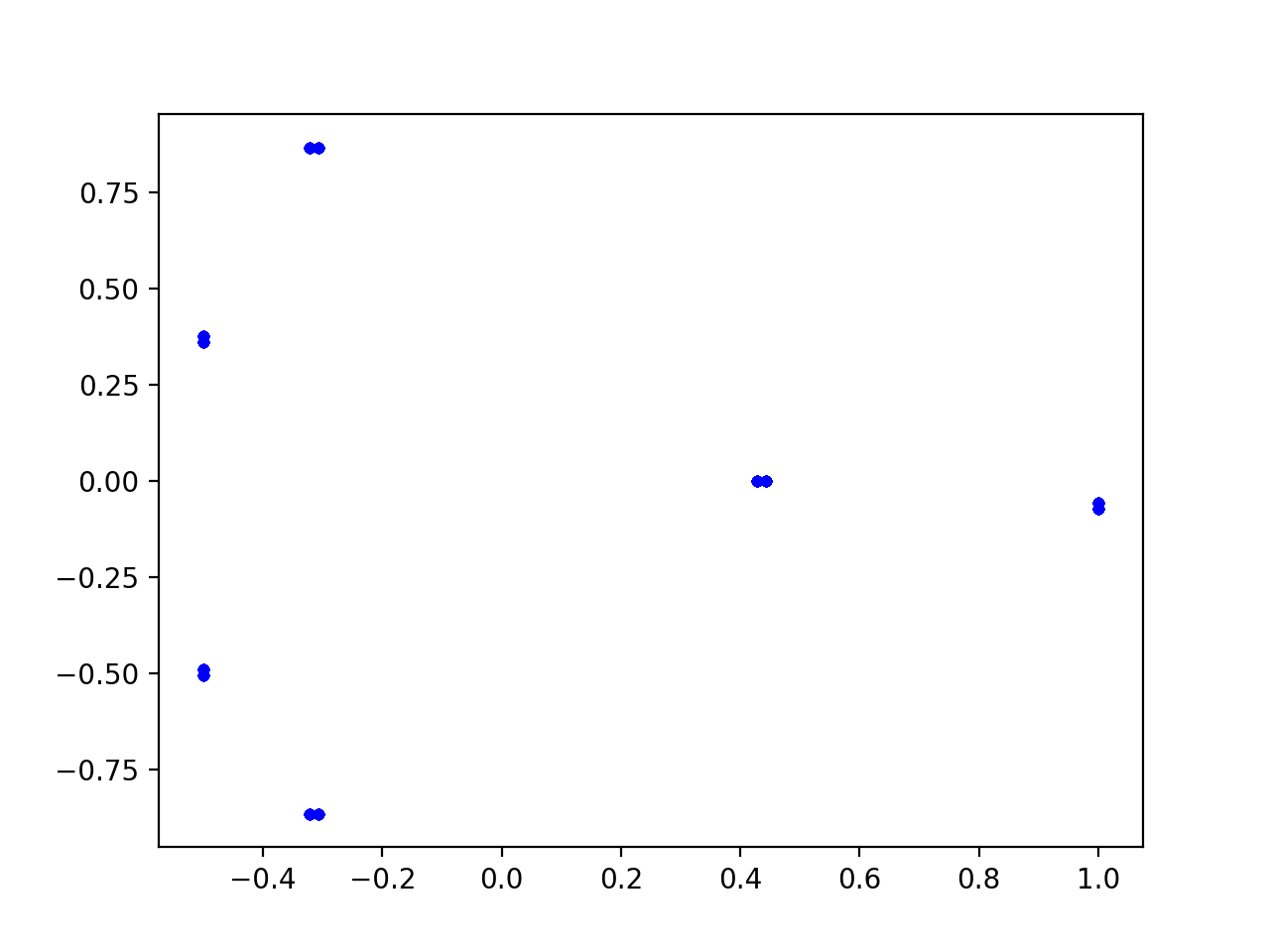
I am trying to generate a Spierpinki Triangle in Python using the Chaos game. The computations of the points to plot seem correct however, instead of thousands of points plotted, only 10 or so are plotted.

import math
import numpy as np
import random as rand
import matplotlib.pyplot as plt

# Defining vertices
t = np.linspace(0, (2 * math.pi), 4)
v = np.array([[math.cos(t[0]), math.cos(t[1]), math.cos(t[2])],
              [math.sin(t[0]), math.sin(t[1]), math.sin(t[2])]])

# Defining Starting point
T = np.array([[0.5, 0], [0, 0.5]])
x = np.array([rand.random() - 0.5, rand.random() - 0.5]).reshape(2, 1)

res = np.zeros((2, 1))
n = 10000
for i in range(n):
    for j in range(2):
        k = rand.randint(0, 2)
        res = np.expand_dims(res, axis=0)
        res = np.multiply(T, np.subtract(x[j], v[:, k]))   v[:, k]
        xx = [x for (x, y) in res]
        yy = [y for (x, y) in res]
        plt.plot(xx, yy, 'b.')

plt.show()

Sierpinksi Triangle Plot

CodePudding user response：

First of all, welcome to SO. Your problem is well-explained. Your code is self-contained. What a great first question.

The computations of the points to plot seem correct.

Not quite. There are multiple issues with your code. Some are actual mistakes, albeit easy to make ones. For example, rand.randint(0,2) gives you a random integer on the interval [0, 2). Notice that you can never get a 2 this way, and your third vertex is never selected.

The much bigger problem is the complexity of your code. An inner loop over j that doesn't change anything. Matrix multiplication to subtract 2 points from one another. Etc. It gets so complicated, that you never notice that x/res never gets updated, such that you are plotting the same points over and over again. You should strive to express ideas simpler. Elegant mathematical notation can be a starting point for your code but it is rarely the endpoint.

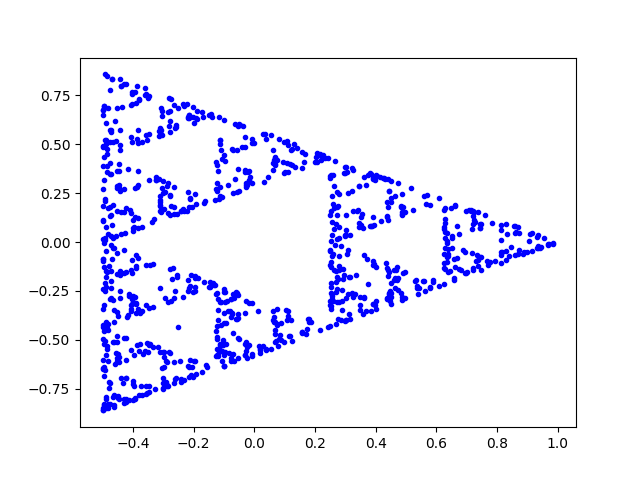
Here is my version of your code, simplified.

import numpy as np
import matplotlib.pyplot as plt

# Defining vertices
t = np.linspace(0, (2 * np.pi), 4)
v = np.array([[np.cos(t[0]), np.cos(t[1]), np.cos(t[2])],
              [np.sin(t[0]), np.sin(t[1]), np.sin(t[2])]])

# Defining Starting point
x = np.array([0., 0.])

# Loop
for k in np.random.randint(3, size=1000):
    x  = 0.5 * (v[:, k] - x)
    plt.plot(x[0], x[1], 'b.')

plt.show()