The method is given NxN matrix always powers of 2 and a number,it will return true if the num is found example for 4x4 size: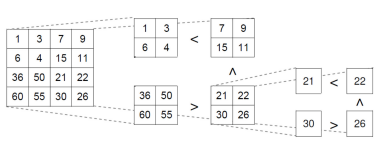

this is what i wrote:

public class Search {
public static boolean Search (int [][] matrix, int num) 
{
int value = matrix.length / 2;
int first_quarter_pivot = matrix[value-1][0]; // represents highest number in first quarter
int second_quarter_pivot = matrix[value-1][value]; // represents highest number in second quarter
int third_quarter_pivot = matrix[matrix.length-1][value]; // represents highest number in third quarter
int fourth_quarter_pivot = matrix[matrix.length-1][0]; // represents highest number in fourth quarter
boolean isBoolean = false; 
int i=0;
int j;  



// if the num is not in the range of biggest smallest number it means he can`t be there.    
 if(!(num >= first_quarter_pivot) && (num <= fourth_quarter_pivot)) {
 return false;
}
// if num is one of the pivots return true;
if((num == first_quarter_pivot || (num ==second_quarter_pivot)) 
|| (num == third_quarter_pivot) || (num == fourth_quarter_pivot ))
return true;

// if num is smaller than first pivot it means num is the first quarter,we limit the search to first quarter.
// if not smaller move to the next quarter pivot
if(num < first_quarter_pivot){{
    j =0;
    do
   
        if(matrix[i][j] == num) {
               isBoolean = true;
               break;
               
               
            }
           else if((j == value)) {
                        j = 0;
                        i  ;
                    }
                        else if(matrix[i][j] != num){
                         j  ;
                        }
                        while(isBoolean != true) ;
                    }
      
              return isBoolean;

            }

    
// if num is smaller than second pivot it means num is the second quarter,we limit the search to second quarter.
// if not smaller move to the next quarter pivot    
if(num < second_quarter_pivot){{
    j = value;// start (0,value) j   till j=value
    do
    
        if(matrix[i][j] == num) {
               isBoolean = true;
               break;
            }
           else if((j == matrix.length-1)) {
                        j = value;
                        i  ;
                    }
                        else if(matrix[i][j] != num){
                         j  ;
                        }
                        while(isBoolean != true) ;
               
}
return isBoolean;
}
            
            // if num is smaller than third pivot it means num is the third quarter,we limit the search to third quarter.
// if not smaller move to the next quarter pivot
            
if(num < third_quarter_pivot){{
i = value;              
j = value;// start (0,value) j   till j=value
    do
    
        if(matrix[i][j] == num) {
               isBoolean = true;
               break;
            }
           else if((j == matrix.length-1)) {
                        j = value;
                        i  ;
                    }
                        else if(matrix[i][j] != num){
                         j  ;
                        }
                        while(isBoolean != true) ;
           
            }
 return isBoolean;
      
  }     
          // if num is smaller than fourth pivot it means num is the fourth quarter,we limit the search to fourth quarter.
// number must be here because we verfied his existence in the start.
  if(num < fourth_quarter_pivot){
    i = value;              
    j = 0;// start (0,value) j   till j=value
    do
    
        if(matrix[i][j] == num) {
               isBoolean = true;
               break;
            }
           else if((j == value)) {
                        j = 0;
                        i  ;
                    }
                        else if(matrix[i][j] != num){
                         j  ;
                        }
                        while(isBoolean != true) ;
 
} 
return isBoolean;    

}

}

What i tried to do: find in which quarter the wanted number is in,after that check the same quarter by moving j until it hits the limit,than i until found with the limits changing for each quarter,i cant understand if run time complexity is O(n^2) or lower? and will it be better do create one dimensional array and and move on the quarter this way: move right until limit,one down,move left until limit and il have a sorted array and just binear search

CodePudding user response：

If you can map an array to a matrix, you can use a normal binary search.

You can define the translation table to achieve that like this:

X = [0, 0, 1, 1, 0, 0, 1, 1, 2, 2, 3, 3, 2, 2, 3, 3, ...]
Y = [0, 1, 1, 0, 2, 3, 3, 2, 2, 3, 3, 2, 0, 1, 1, 0, ...]

The final program looks like this.

static final int MAX_N = 64;
static final int MAX_NN = MAX_N * MAX_N;
static final int[] DX = {0, 0, 1, 1};
static final int[] DY = {0, 1, 1, 0};
static final int[] X = new int[MAX_NN];
static final int[] Y = new int[MAX_NN];

static {  // initialize X and Y
    for (int i = 0; i < MAX_NN;   i) {
        int x = 0, y = 0;
        for (int t = i, f = 0; t > 0;   f) {
            int mod = t & 3;
            x  = DX[mod] << f; y  = DY[mod] << f;
            t >>= 2;
        }
        X[i] = x; Y[i] = y;
    }
}

public static boolean Search(int [][] matrix, int num) {
    int n = matrix.length, nn = n * n;
    int lower = 0;
    int upper = nn - 1;
    while (lower <= upper) {
        int mid = (lower   upper) / 2;
        int value = matrix[X[mid]][Y[mid]];
        if (value == num)
            return true;
        else if (value < num)
            lower = mid   1;
        else
            upper = mid - 1;
    }
    return false;
}

and

public static void main(String[] args) {
    int[][] matrix = {
        {1, 3, 7, 9},
        {6, 4, 15, 11},
        {36, 50, 21, 22},
        {60, 55, 30, 26},
    };
    // case: exists
    System.out.println(Search(matrix, 1));
    System.out.println(Search(matrix, 60));
    System.out.println(Search(matrix, 11));
    // case: not exists
    System.out.println(Search(matrix, 0));
    System.out.println(Search(matrix, 70));
    System.out.println(Search(matrix, 20));
}

output:

true
true
true
false
false
false