My given string is "Today_is_Monday". If I apply Huffman's coding algorithm to this string. Without encoding, the total size of the string was (15*8) = 120 bits. After encoding the size is (10*8 15 49) = 144 bits.

As I know Huffman's algorithm uses to reduce size. But why the encoded size is more than its original?

More details I have done are given below

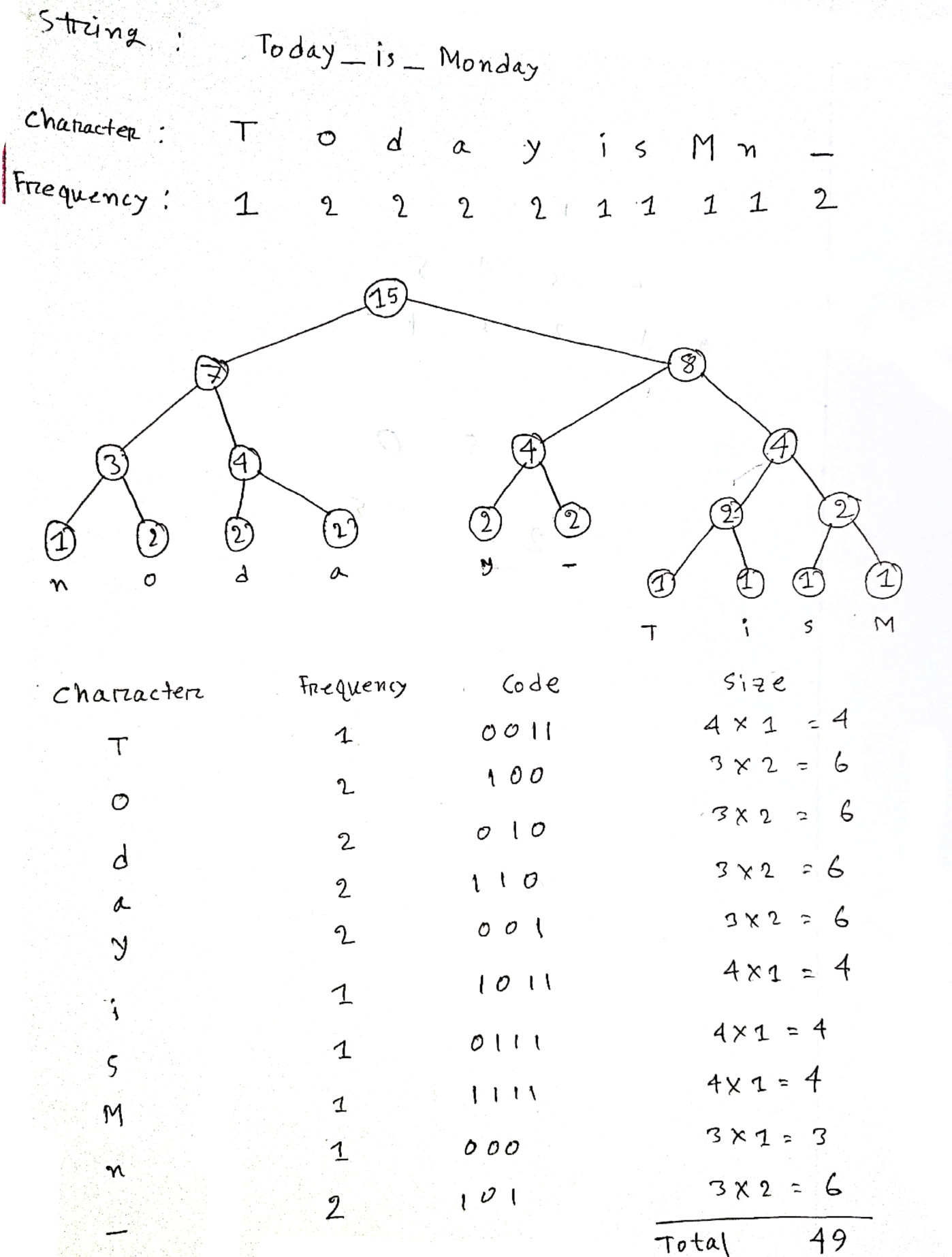
Thank you.

CodePudding user response：

The text is too short and the probability distribution function looks uniform. If the frequencies of occurrence are (more or less) the same, the input string gets very close to random noise. It is impossible to compress random noise in a general way, compression will most likely be longer than the input sequence, because one also need to add some metadata, like an encoding table.

In contrast, consider encoding a string that is: aaaaaaaaaaaaaaa.

If one tries to encode a longer general English text, one would notice at some point, the encoded string size will start to get dramatically shorter than the original text. This is because the encoded sequence frequencies will start to make a much higher impact - the most frequent character will be encoded with the shortest possible code and because it is repeated a lot, its shorter size will dominate the size of the original character.

CodePudding user response：

Huffman encoding optimizes the message length, given the frequency table. What you do with the frequency table is up to you.

Applications for very short messages often assume a static frequency table that both the transmitter and receiver know in advance, so it doesn't have to be transmitted.

Applications that need to send the frequency table often perform additional optimization. It's possible to communicate the tree by transmitting just the lengths of each symbol in alphabetical order. The lengths themselves can then be Huffman-encoded.

CodePudding user response：

There is no reversible compression algorithm that is guaranteed to compress all possible inputs. If there was, then you could repeatedly feed it its own output and eventually reduce any input file to 1 bit. For any initial input file.

Hence, there must be some inputs that cannot be compressed by any particular algorithm.

As others have explained, you have found an input that Hoffman cannot compress.