Matrix Multiplication in python vs R not returning the same results for SVD whitening-CodePudding

I'm trying

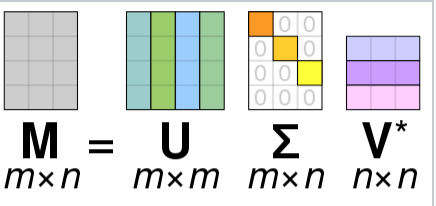
And this is what you get back in scipy.linalg.svd:

Factorizes the matrix a into two unitary matrices U and Vh, and a 1-D array s of singular values (real, non-negative) such that a == U @ S @ Vh, where S is a suitably shaped matrix of zeros with main diagonal s.

Whereas for svd in R they return you V. Therefore should be:

Vt = t(internal$v)

Then in R:

ZCA_svd(x)

 head(ZCA_svd(x))
            [,1]        [,2]        [,3]        [,4]        [,5]        [,6]
[1,]  0.26067006  0.02112997  0.09365719  0.01843731  0.05470893  0.01750415
[2,] -0.17174605 -0.23530453  0.15122167 -0.27738192  0.03830312 -0.21142466
[3,] -0.10659408  0.07042392  0.06732517 -0.12081178  0.09487670 -0.01726953
[4,]  0.10659431  0.13668984  0.18523379  0.03799714  0.06525643 -0.09888497
[5,] -0.12998931 -0.05254591 -0.14654516 -0.15600721  0.13455552 -0.09930468
[6,] -0.07010493  0.01084335 -0.05152612 -0.07803706 -0.03505320  0.43416503
            [,7]        [,8]        [,9]
[1,] -0.02021101  0.08766270 0.073049749
[2,]  0.15877490  0.24157032 0.009806777
[3,]  0.03148085  0.09361557 0.100372380
[4,] -0.03620529  0.09898168 0.044607751
[5,]  0.02847737 -0.30396604 0.574410291
[6,]  0.03105272  0.13842155 0.076071540

In python:

pd.DataFrame(svd_whiten(df.iloc[:,2:])).head(6)
 
          0         1         2         3         4         5         6         7         8
0  0.260670  0.021130  0.093657  0.018437  0.054709  0.017504 -0.020211  0.087663  0.073050
1 -0.171746 -0.235305  0.151222 -0.277382  0.038303 -0.211425  0.158775  0.241570  0.009807
2 -0.106594  0.070424  0.067325 -0.120812  0.094877 -0.017270  0.031481  0.093616  0.100372
3  0.106594  0.136690  0.185234  0.037997  0.065256 -0.098885 -0.036205  0.098982  0.044608
4 -0.129989 -0.052546 -0.146545 -0.156007  0.134556 -0.099305  0.028477 -0.303966  0.574410
5 -0.070105  0.010843 -0.051526 -0.078037 -0.035053  0.434165  0.031053  0.138422  0.076072