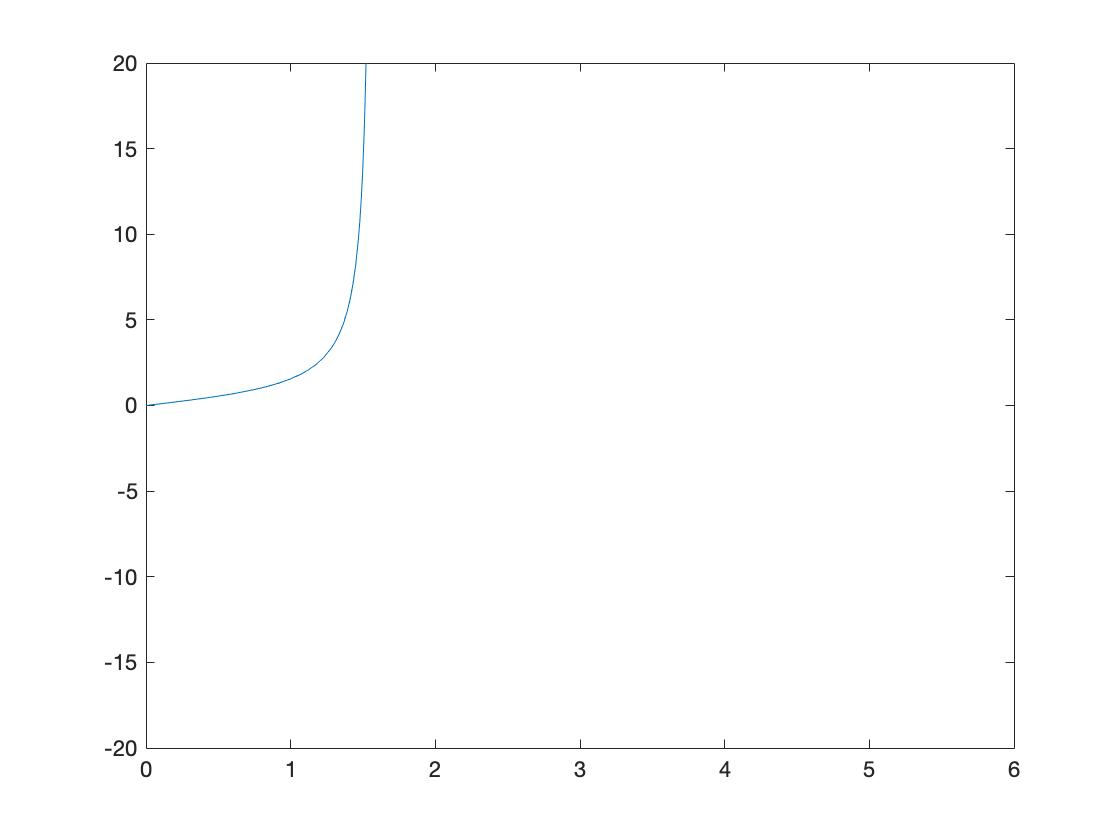
I would like to use numerical approach to calculate the differential with singularities.

For instance, y'=y^2 1 with y(0)=0. The analytical solution is not hard to find, y=tan(x).

The problem arises when I apply the numeric method, see the code in Matlab

tspan = [0 6];
y0 = [0; 0];
ode = @(t, y) y.^2 1;
[t, y] = ode45(ode, tspan, y0);
plot(t, y(:,1))
axis([0 6 -20 20])

which gives the plot below, i.e., it missed the part of solution after the first singularity.

My question: how to find the full numeric solution of a differential equation with singularities?

Thanks in advance!

CodePudding user response：

This is impossible in general. An ODE solution ends where it diverges to infinity (or leaves the domain of the ODE function in any other way).

What you can do is apply domain knowledge. This equation is a Riccati DE. If one knows one solution, one can transform it into a Bernoulli DE that has a solution formula. There is a second transform without knowledge of a particular solution, it works always but is not always helpful. Set y=p/q and select their relationship so that a system of linear equations results. Here p'q-q'p=p^2 q^2 resolves nicely to p'=q, q'=-p, or as second order DE u'' u=0, the harmonic oscillator, for u=q or u=p. This system now has no singularities and the poles of the original solution y are the roots of the denominator q.