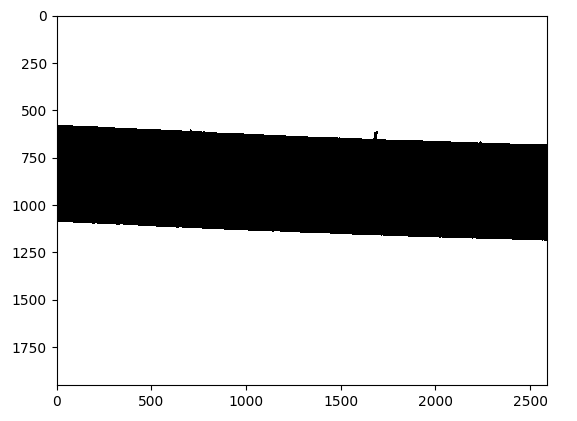
I am currently working on a measurement system that uses quantitative image analysis to find the diameter of plastic filament. Below are the original image and the processed binary image, using DipLib (PyDIP variant) to do so.

The Problem

Okay so that looks great, in my personal opinion. the next issue is I am trying to calculate the distance between the top edge and the bottom edge of the filament in the binary image. This was pretty simple to do using OpenCV, but with the limited functionality in the PyDIP variant of DipLib, I'm having a lot of trouble.

Potential Solution

Logically I think I can just scan down the columns of pixels and look for the first row the pixel changes from 0 to 255, and vice-versa for the bottom edge. Then I could take those values, somehow create a best-fit line, and then calculate the distance between them. Unfortunately I'm struggling with the first part of this. I was hoping someone with some experience might be able to help me out.

Backstory

I am using DipLib because OpenCV is great for detection, but not quantification. I have seen other examples such as this one

Notice the variables defined above, y1_1, y1_2, y2_1, and y2_2. Using them, you can get the diameter from both ends of the filament:

print(y1_2 - y1_1)
print(y2_2 - y2_1)

Output:

100
105

CodePudding user response：

I think the most precise approach to measure the distance between the two edges of the filament is to:

1. detect the two edges using the Gaussian gradient magnitude,
2. determine the center of gravity of the two edges, which will be a point on each of the edges,
3. determine the angle of the two edges, and
4. use trigonometry to find the distance between the two edges.

This assumes that the two edges are perfectly straight and parallel, which doesn't seem to be the case though.

Using DIPlib you could do it this way:

import diplib as dip
import numpy as np
import matplotlib.pyplot as pp

# load
img = dip.ImageRead('wDnU6.jpg') 
img = img(1)  # use green channel
img.SetPixelSize(0.042, "mm")

# find edges
edges = dip.GradientMagnitude(img)

# binarize
mask = dip.Threshold(edges)[0]
mask = dip.Dilation(mask, 9)  # we want the mask to include the "tails" of the Gaussian
mask = dip.AreaOpening(mask, filterSize=1000)  # remove small regions

# measure the two edges
mask = dip.Label(mask)
msr = dip.MeasurementTool.Measure(mask, edges, ['Gravity','GreyMajorAxes'])
# msr[n] is the measurements for object with ID n, if we have two objects, n can be 1 or 2.

# get distance between edges
center1 = np.array(msr[1]['Gravity'])
center2 = np.array(msr[2]['Gravity'])

normal1 = np.array(msr[1]['GreyMajorAxes'])[0:2]  # first axis is perpendicular to edge
normal2 = np.array(msr[2]['GreyMajorAxes'])[0:2]
normal = (normal1   normal2) / 2  # we average the two normals, assuming the edges are parallel

distance = abs((center1 - center2) @ normal)
units = msr['Gravity'].Values()[0].units
print("Distance between lines:", distance, units)

This outputs:

Distance between lines: 21.491425398007312 mm

You can show the two edges with:

mmpp = img.PixelSize()[0].magnitude
center1 = center1 / mmpp  # position in pixels
center2 = center2 / mmpp
L = 1000
v = L * np.array([normal[1], -normal[0]])
img.Show()
pt1 = center1 - v
pt2 = center1   v
pp.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])
pt1 = center2 - v
pt2 = center2   v
pp.plot([pt1[0], pt2[0]], [pt1[1], pt2[1]])

Another approach uses the distance transform, which assigns to each object pixel the distance to the nearest background pixel. Because the filament is approximately horizontal, it is easy to use the maximum value for each image column as half the width at one point along the filament. This measurement is a bit noisy, because it computes distances between pixels, and uses a binarized image. But we can average the width for each image column to obtain a more precise measurement, though it is likely biased (the estimated value is likely smaller than the true value):

mask = dip.Threshold(img)[0]
dt = dip.EuclideanDistanceTransform(mask, border='object')
width = 2 * np.amax(dt, axis=0)
width = width[100:-100]  # close to the image edges the distance could be off
print("Distance between lines:", np.mean(width), img.PixelSize()[0].units)

This outputs:

Distance between lines: 21.393684 mm

You could also compute locally averaged widths, if you suspect that the filament is not uniform in width:

width_smooth = dip.Gauss(width, 100)

You could then plot the estimated widths to see your estimates:

pp.plot(width)
pp.plot(width_smooth)
pp.show()