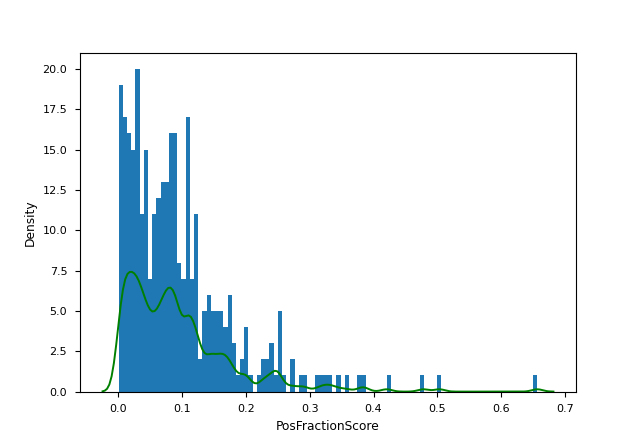
Hi all, I am trying to sample random values from between 0 and 1, with weights provided by datases like the one above. I have found a partial solution to this problem using scipy.stats.gaussian_kde and its .resample(n) method. My main issue is that, because the bulk of my data is so close to 0, resampling returns a bunch of negative numbers that mess up my later calculations.

Is there a way to limit my resampling to be all greater than zero, without otherwise changing sample space? I have considered just taking the absolute value of everything to get rid of negatives, but I don't know if that would be reflective of the distribution weights.

And to clarify, each value that I resample (n) will correspond to a specific variable in my code, so I can't just delete numbers that are less than zero.

# Here is a little sample dataset if you need something to work this out!
import numpy as np
data = np.array([0.147, 0.066, 0.017, 0.011, 0.040, 0.087, 0.024, 0.127, 0.071, 0.127,
                 0.027, 0.008, 0.067, 0.032, 0.247, 0.028, 0.122, 0.304, 0.074, 0.119])
# Thank you!

CodePudding user response：

You could use a distribution whose support does not include negative numbers. For example, sampling from an exponential distribution might work for the example array you provided:

import numpy as np
from scipy.stats import expon
import matplotlib.pyplot as plt

data = np.array([0.147, 0.066, 0.017, 0.011, 0.040, 0.087, 0.024, 0.127, 0.071, 0.127, 0.027, 0.008, 0.067, 0.032, 0.247, 0.028, 0.122, 0.304, 0.074, 0.119])

# fit exponential model using data
loc, scale = expon.fit(data)

# plot histogram and model
fig, ax = plt.subplots()
ax.hist(data, density = True)
x = np.linspace(0.01, 1, 200)
ax.plot(x, expon.pdf(x, loc, scale), 'k-')
plt.show()

# sample from your modelled distribution using your fitted loc and scale parameters
sample = expon.rvs(loc, scale)

CodePudding user response：

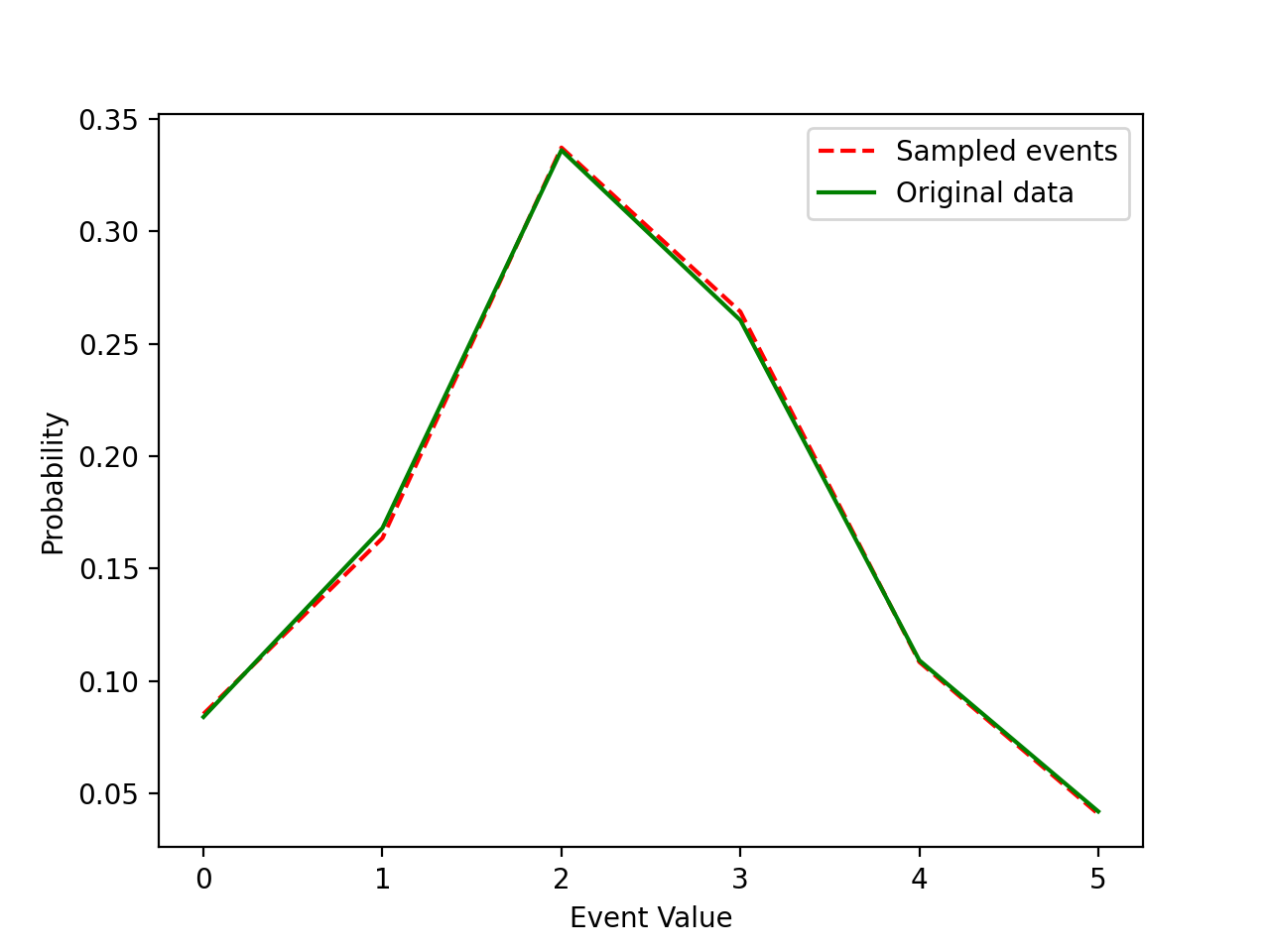
You can use either rejection sampling or Inverse Transform Sampling to sample your data directly. This algorithm has 4 steps:

1. Compute the cumulative distribution function CDF of your data.
2. Sample a random number u from a uniform distribution over the interval [0,1].
3. Find the inverse InverseCDF of your CDF.
4. Compute X = InverseCDF(u) where X will be distributed as CDF(X).

Here's a Python sample code using NumPy to illustrate the algorithm:

import numpy as np
import numpy.random as ra
from matplotlib import pyplot as plt


'''
Step 1: Compute cumulative distribution function
'''
data = [[1, 2, 3, 4, 5, 6],[100, 200, 400, 310, 130, 50]]
event_value = np.array(data[0])
event_frequency = np.array(data[1])

prob = event_frequency/float(sum(event_frequency))
cum_prob = np.cumsum(prob)
print(prob)
print(cum_prob)

'''
Step 2: Sample uniform random numbers
'''
N = 10000
U = ra.uniform(0, 1, N)


'''
Step 3: Generate Samples from Inverse CDF:
'''
sample_x = [int(event_value[np.argwhere(cum_prob == min(cum_prob[(cum_prob - u) > 0]))]) for u in U]


'''
Step 4: Comparison
'''
sample_x = (np.array(sample_x)-1).astype(int)
times = np.arange(0,6,1)
lc = np.bincount(sample_x, minlength=len(times))

plot1, = plt.plot(lc/float(sum(lc)), 'r--', label='Sampled events')
plot2, = plt.plot(prob,'g',label='Original data')
plt.xlabel('Event Value')
plt.ylabel('Probability')
plt.legend(handles=[plot1,plot2])
plt.show()

Output:

CodePudding user response：

To complete the answer from Ben Devries, you have several options to manage this situation. You're confronted to a distribution which has a cut-off at zero (let's point out this might not be the case, but knowing your data, you seem sure it's impossible, which is ok !). Gaussian KDE don't handle that very well, because they are usually defined over the real space.

A wise option is to switch from KDE to parametric estimation. That means you assume a form of the probability density (based on the form of the data and your knowledge of their origin) and try to tune the probability density parameters (loc and scale for many distributions for instance) so that the density fits the data. In your case, the distribution looks like an exponential, a lot.

If you have no clue, you can try to stick to a KDE (a form of non-parametric estimation by the way), and manage the cut-off using random variables transformations: you try to apply a function to your data so that it can be easily fitted by a KDE, and easily turned back to the original distribution afterwards.

There, a log transform seems to be the perfect function to apply. A link for the detail: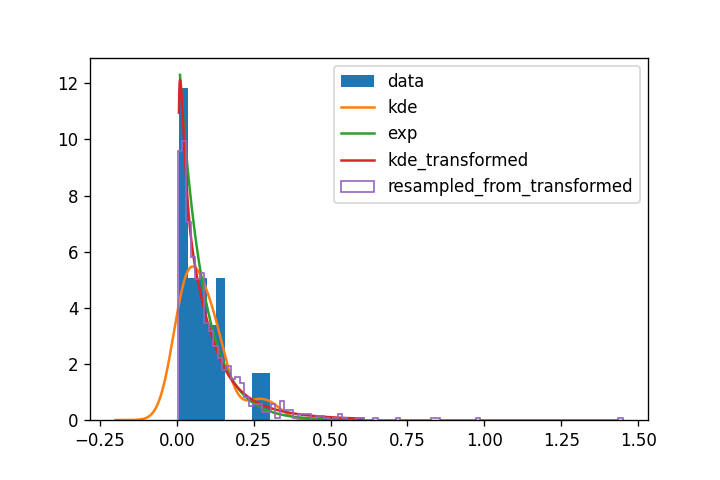

As you can see:

• the exponential match the transformed KDE a lot. That seems a safe option.
• the transformed KDE does not exhibit a sharp cut-off like the exponential fit around 0 ; that's typical of the technique I think (https://stats.stackexchange.com/questions/403532/can-kernel-density-estimation-estimate-an-exponential-distribution for more details)