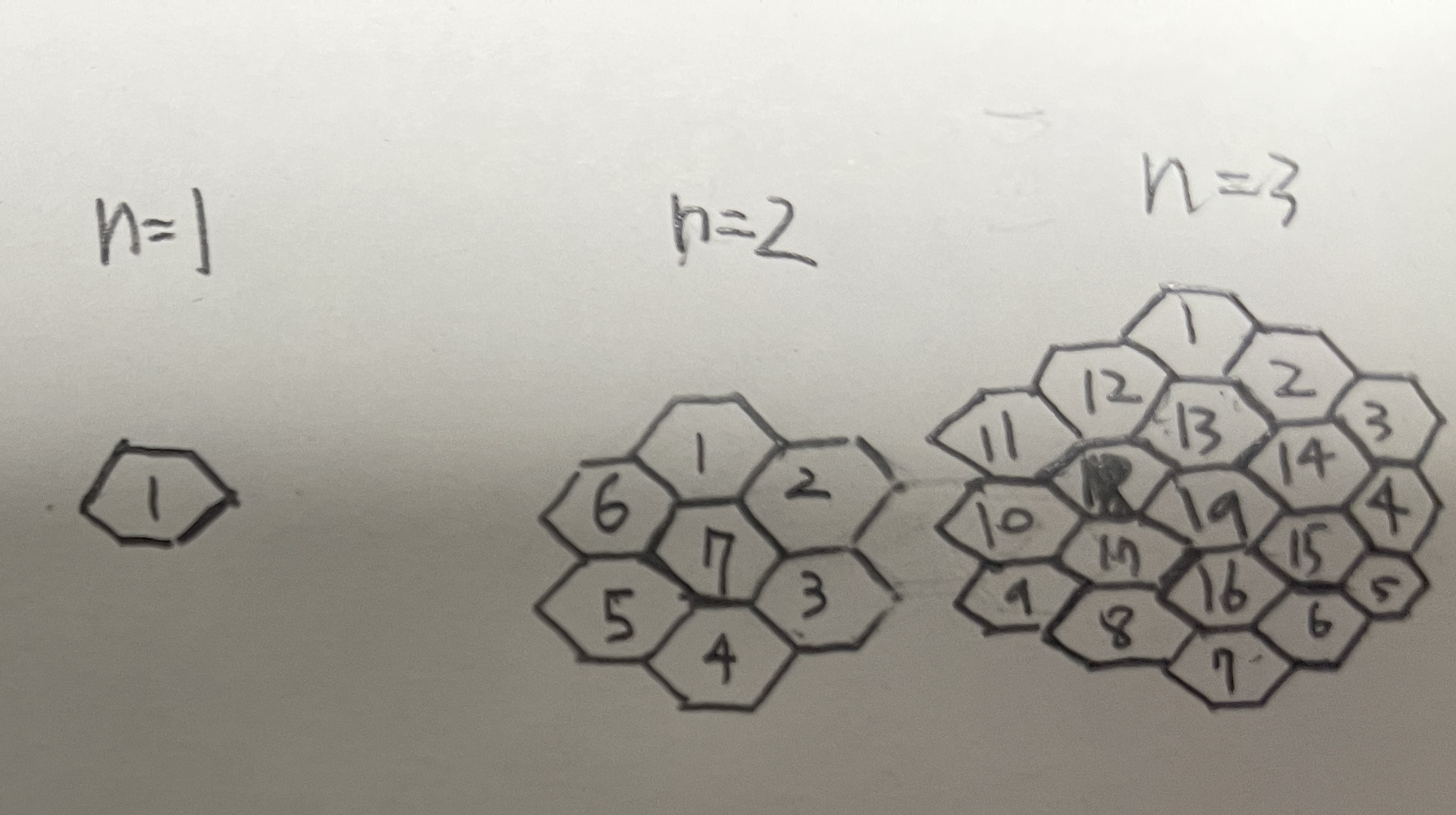
The regular hexagon sequence is defined as follow.

1. The highest hexagon is 1.
2. next hexagon is on clockwise of previous hexagon.
3. if next hexagon already has number, then inner highest hexagon is given number.
4. The sequence is generated by reading of all hexagon from top left to bottom right. For example, sequences are when n=1, 1 when n=2, 1-6-2-7-5-3-4 when n=3, 1-12-2-11-13-3-18-14-10-19-4-17-15-9-16-5-8-6-7

how to generate regular hexagon sequence of n?

CodePudding user response：

I used some observations:

1. Notice that number of required rows is 4 * n - 3
2. Notice that to represent a row we need 2 vectors:

• if we are on the right side of a hexagon, we append in front of that array
• if we are on the left side of a hexagon, we append to the right of that array

3. Notice that if we are on the right side of a hexagon we need to jump 1 row down, and if we are on the left side, we need to jump a row up
4. Notice that if we are on the vertical edge of a hexagon (either left or right) we need to jump 2 rows: left vertical we jump 2 rows up, right vertical we jump 2 rows down

from collections import deque

def hexagon_pattern(n):
    if n == 1:
        return [1]

    # Denotes how many rows we need
    n_rows = 4 * n - 3
    
    # Create a row as a tuple of left half and right half
    # This is done as if we are in the right half of the
    # hexagon, we append to the left, otherwise we append to
    # the right
    rows = [(deque([]), deque([])) for i in range(n_rows)]
    
    # Denotes the dimension of a line (how many numbers)
    # we push to a line
    # Obs: this starts from n - 1 and continues to 0
    # If this is 0, it means we have to fill in only the number
    # in the center of the hexagon
    line_dim = n - 1
    
    # Denotes the number that needed to be introduced in the pattern
    crt_num = 1
    
    # Start row to the current hexagon
    # Obs: the start row of next hexagon is at a distance of 2
    # from the previous start row of the previous hexagon
    start_row = 0
    
    # We have n hexagon patterns to fill in
    while n:
        # Every hexagon pattern start at a different row
        crt_row = start_row
        
        # Indicator that we are at the middle number
        if line_dim == 0:
            rows[crt_row][0].append(crt_num)
            break

        # For every level we have a hexagon
        for line_no in range(6):
            # We have to fill in the hexagon edge
            for _ in range(line_dim):
                if crt_row >= n_rows:
                    continue
                
                if line_no < 3:
                    # We are on the right part of a hexagon (first 3 edges)
                    rows[crt_row][1].appendleft(crt_num)
                else:
                    # We are on the left part of a hexagon (last 3 edges)
                    rows[crt_row][0].append(crt_num)
                
                # Increment the number to be added in pattern
                crt_num  = 1
                
                # If we are on the right vertical line of the hexagon, then we jump 2 lines down
                if line_no == 1:
                    crt_row  = 2
                # If we are on the left vertical line of the hexagon, then we jump 2 lines up
                elif line_no == 4:
                    crt_row -= 2
                # If we are on the right side of the hexagon we jump one line down
                elif line_no < 3:
                    crt_row  = 1
                # If we are on the left side of the hexagon we jump one line up
                else:
                    crt_row -= 1
        
        n -= 1
        line_dim -= 1
        start_row  = 2
    
    # We concatenate the two halves of every row
    # After that, we concatanate all the sublists in a single list
    result = sum(list(filter(lambda l: l, map(lambda t: list(t[0]   t[1]), rows))), [])
    
    return result
            
if __name__ == '__main__':
    print(hexagon_pattern(1))
    print(hexagon_pattern(2))
    print(hexagon_pattern(3))