Map an array of N 2D coordinates into an array of N 2D grids/images-CodePudding

My input is a set of N 2D coordinates in the form of a numpy array, e.g.:

import numpy as np
import matplotlib.pyplot as plt

X = np.array([
  [-5, 1],
  [3, 7.2],
  [0, -7],
  [9, -8],
  [0, 0.1]
])

Here N would be 5 coordinates.

We can bin each point to some resolution X resultion 2D grid parameter on the 2D field for which we know the min_X and max_X for both dimensions:

resultion = 100
min_X = -10
max_X = 10
bins = np.linspace(min_X, max_X, resolution   1)
X_binned = np.digitize(X, bins) - 1
X_binned

array([[25, 55],
      [65, 86],
      [50, 15],
      [95, 10],
      [50, 50]], dtype=int64)

So for example here we have a 100 X 100 grid on the [-10,10] X [-10,10] field, and point (-5, 1) maps to cell (25,55).

Now I would like a set of 2D all-zero grids, in the form of a N X resolution X resolution X 1 numpy array (or a set of "images"). For each grid i there should appear 1 for coordinate i location.

This is what I'm doing but it seems not very numpy-y and the complexity is O(N) (N would eventually be around 100K):

X_images = np.zeros((X.shape[0], resolution, resolution, 1), dtype=np.uint8)
for i, (j, k) in enumerate(X_binned):
    X_images[i, resolution - 1 - k, j, 0] = 1

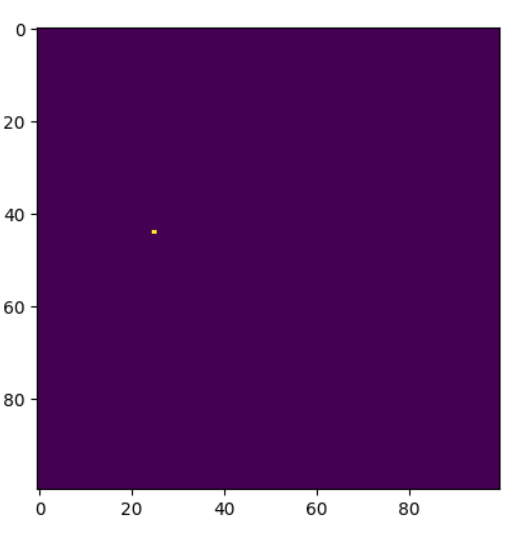
To show that it works see e.g. first point (-5, 1) which maps to where it should be on the X_images[0] grid/image:

plt.imshow(X_images[0])
plt.show()

So is there a better way, if not more efficient more elegant?

CodePudding user response：

You can set them all at once by indexing X_images with the list of rows and cols:

X_images = np.zeros((X.shape[0], resolution, resolution, 1), dtype=np.uint8)

i = np.arange(X.shape[0])
j = X_binned[:, 0]
k = resolution - 1 - X_binned[:, 1]

X_images[i, k, j] = 1

CodePudding user response：

Using np.ix_() makes this pretty straight forward:

X_images = np.zeros((X_binned.shape[0], 100, 100, 1), dtype="uint8")
X_images[np.ix_(np.arange(N), *X_binned.T, [0])] = 1