Bi-linear interpolation on a trapezoid-CodePudding

I am trying to interpolate data based on an input forming a trapezoid. I found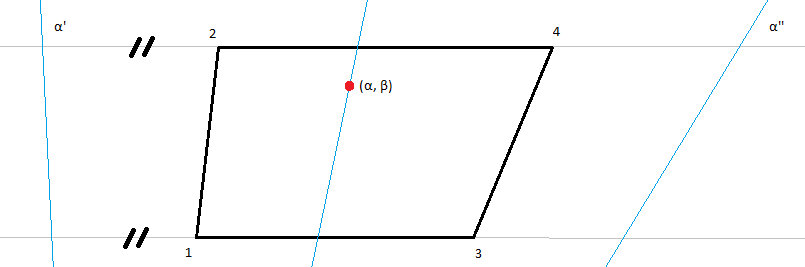

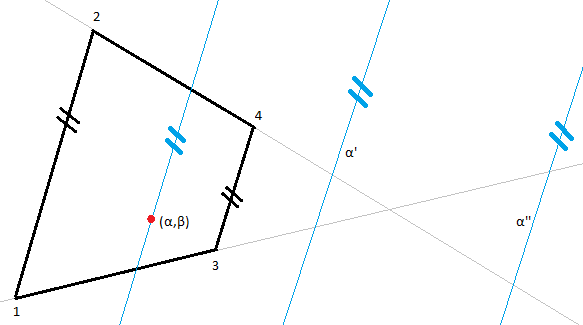
In both configurations (which are equivalent if the parameters are swapped), the blue lines representing different values of alpha never intersect inside the trapezoid itself, which means there cannot be multiple solutions.

The special case solution for trapezoids can be derived from the original expressions for the interpolated coordinate R:

R = (1 - β)*[(1 - α)*P1   α*P3]   β*[(1 - α)*P2   α*P4]

  = (1 - β)*[P1   α*(P3 - P1)]   β*[P2   α*(P4 - P2)]

  = P1   β*(P2 - P1)   α*(P3 - P1)   αβ*(P4 - P3 - P2   P1)

  = P1   β*E12   α*E13   αβ*(E24 - E13)

where the "edge vector" Exy = Py - Px

Moving P1 to the LHS, and taking the cross-product of both sides with edges 1-2 and 1-3:

(R - P1)xE12 = β*E12xE12   α*E13xE12   αβ*(E34xE12 - E12xE12)
------------     -------     -------       -------   -------
      A            = 0          C             E        = 0
   
(R - P1)xE13 = β*E12xE13   α*E13xE13   αβ*(E24xE13 - E13xE13)
------------     -------     -------       -------   -------
      B             D          = 0            F        = 0

Recalling that the cross-product of parallel vectors equals 0. Arriving at a pair of simultaneous quadratic equations:

A = α*C   αβ*E
B = β*D   αβ*F

note that D = -C

In the first diagram, E13 and E24 are parallel, which means F = 0:

β = B/D
α = A / (C   E*B/D) = A*C / (C*C - E*B)

... and ditto for the second.