I have a 2D geometry which is specified by a number of facets where each facet is a triangle specified by 3 vertex coordinates like facet = [[0, 0], [1, 0], [1, 1]].
I can plot these in matplotlib by converting each facet into a Polygon patch and plotting those patches. However, I would like an algorithm that takes my list of facets and converts into a single closed polygon path of all exterior vertices.
For example suppose I have
facet_list = [[[0, 0], [1, 0], [1, 1]],
[[0, 0], [1, 1], [0, 1]],
[[1, 0], [2, 0], [2, 1]],
[[1, 0], [2, 1], [1, 1]],
[[1, 1], [2, 1], [2, 2]],
[[1, 1], [2, 2], [1, 2]]]
solid_vertex_list = [[0, 0],
[1, 0],
[2, 0],
[2, 1],
[2, 2],
[1, 2],
[1, 1],
[0, 1]]
The first dataset is a list of facets while the second dataset is the target list of exterior vertices. See below for visualizations of these two dataset:
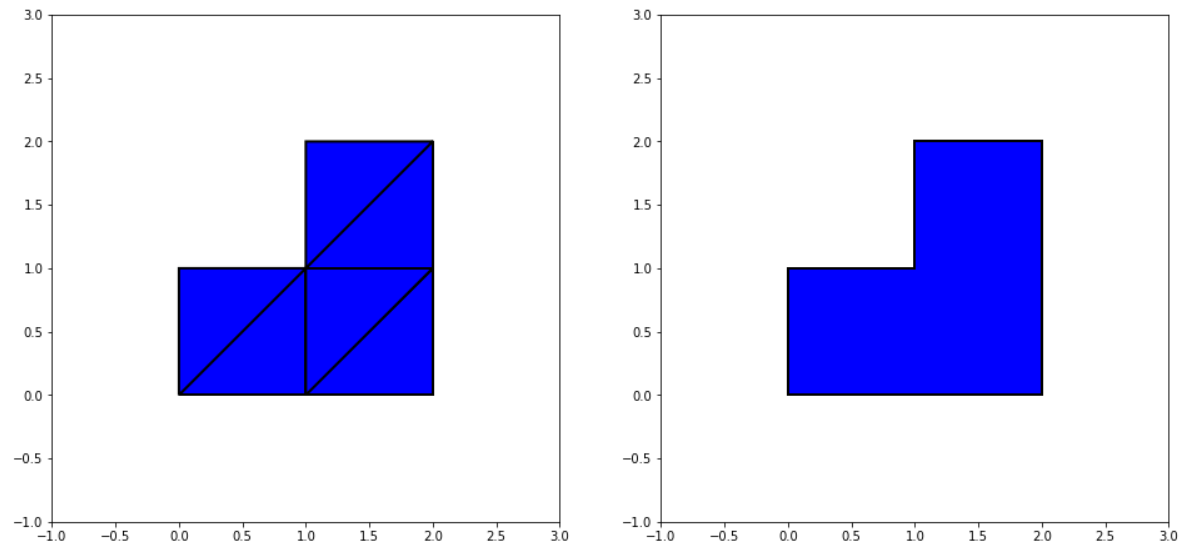
I seek an algorithm that converts the first dataset into the second. There are a few features that are not captured by this specific example but that are desired for the algorithm.
(1) in this example all vertices are exterior vertices, but in general there may be facets that are entirely in the interior of the resulting "large" polygon.
(2) In general the "large" polygon may have holes in it. I'm not sure how best to handle this, but according to this matplotlib documentation, it looks like the matplotlib PathPatch object can plot holes in polygons if you give the vertices for the hole in reverse order. So for purposes of this algorithm it would be sufficient if the vertex paths for any "holes" are simply reported as separate polygons in reverse order.
(3) The facets may form disconnected polygons. In this case separate vertex lists should be returned indicating separate polygons. If two polygons are only connected by a single vertex or less then they are considered to be disconnected.
I think the above 3 points are requirements for the facets -> polygon(s) (with hole(s)) algorithm. In total I think the algorithm would return a list of vertex lists where the vertex lists are listed clockwise if they correspond to disconnect exterior polygons and listed counterclockwise if they correspond to holes. Perhaps there needs to be something indicating which hole corresponds to which exterior polygon. A tricky edge case might be: how to treat a hole that has one or more external vertices. i.e. when a hole touches the exterior at one or more isolated points.
For purposes of this algorithm we can assume that facets share nodes with other facets so that (1) facets are non-overlapping, i.e. no node of any facet is inside another facet and (2) facets only share complete edges, i.e. no node of one facet is part-way along the edge of another facet. A topic for a separate question would be how to take data which does not satisfy (1) and (2) and sanitize it by adding more facets to break up intersections and mid-edge nodes.
CodePudding user response:
I know you call them facets, but that term is overloaded for me. I'll call them triangles instead.
First step, make sure that all triangles have the same orientation. Here is some simple code for that.
def dot (vector1, vector2):
return vector1[0] * vector2[0] vector1[1] * vector2[1]
def vector_from_points (point1, point2):
return [point2[0] - point1[0], point2[1] - point1[1]]
def rotate_vector_90 (vector):
return [-vector[1], vector[0]]
def oriented_triangle (triangle):
vector1 = vector_from_points(triangle[0], triangle[1])
vector2 = vector_from_points(triangle[1], triangle[2])
normal = rotate_vector_90(vector1)
if 0 < dot(normal, vector2):
return triangle
else:
return [triangle[0], triangle[2], triangle[1]]
And now if two triangles share an edge, it is guaranteed that one will be of the form [a, b] and the other of the form [b, a].
So we can just load up a dictionary as follows:
triangle_position = {}
for triangle in triangles:
for i in range(3):
triangle_position[tuple(triangle[i])] = (triangle, i)
And now we can walk through all of the edges. If it is an interior edge, we ignore it. If it is an exterior edge, we can find the next edge in the triangle it is from. While that isn't an exterior edge, we can find the triangle with the reverse edge and move to ITS next edge. Eventually we get to the next exterior edge. This lets us walk around exteriors.
I can guarantee that the outside of shapes will be oriented counterclockwise, and holes within shapes will be oriented clockwise. I can't guarantee what orders holes versus shapes will be found in though - you may need to figure that out for yourself. I'd suggest a ray tracing algorithm.
I won't tackle the bonus question.
CodePudding user response:
Assuming that all triangles have their points given in the same cyclic orientation (either all clockwise or all anticlockwise) you can do the following:
Collect all edges, and only keep those that are not countered by their opposite (so [a, b] gets removed by [b, a]). This way you end up with edges that should belong to a polygon. The edges that remain describe one or more polygons with the same cyclic orientation as the triangles, and zero or more holes with the opposite orientation.
Create an adjacency list for the edges of step 1.
As long as there are non-visited edges, choose an non-visited edge, remove it from the adjacency list, start a new polygon with the starting vertex of this edge, and repeat the following steps to populate the polygon with more vertices:
- mark the edge as visited
- if the ending vertex has no outgoing edge in the adjacency list, exit this loop
- append the ending vertex to the polygon
- extract a neighboring vertex from the adjacency list (and remove it from it)
- repeat from the fist bullet point with this neighboring edge.
Add this polygon to the list of polygons
Repeat from step 3 until all edges have been marked as visited.
Here is code to do that:
def triangles_to_polygons(triangles):
# Collect those edges that are not negated by an opposite edge
edges = set()
for triangle in triangles:
a, b, c = map(tuple, triangle)
for start, end in (a, b), (b, c), (c, a):
if (end, start) in edges:
edges.remove((end, start))
else:
edges.add((start, end))
# Create an adjacency list
adj = {}
for a, b in edges:
adj.setdefault(a, []).append(b)
# Populate polygons
polygons = []
visited = set()
for edge in edges:
if edge not in visited:
a, b = edge
adj[a].remove(b)
polygon = [a]
while True:
visited.add((a, b))
if not adj[b]:
break
polygon.append(b)
a, b = b, adj[b].pop()
polygons.append(polygon)
return polygons
An example run:
triangles = [[[0, 0], [1, 0], [1, 1]],
[[0, 0], [1, 1], [0, 1]],
[[1, 0], [2, 0], [2, 1]],
[[1, 0], [2, 1], [1, 1]],
[[1, 1], [2, 1], [2, 2]],
[[1, 1], [2, 2], [1, 2]]]
polygons = triangles_to_polygons(triangles)
print(polygons)
