Keyframe animations in

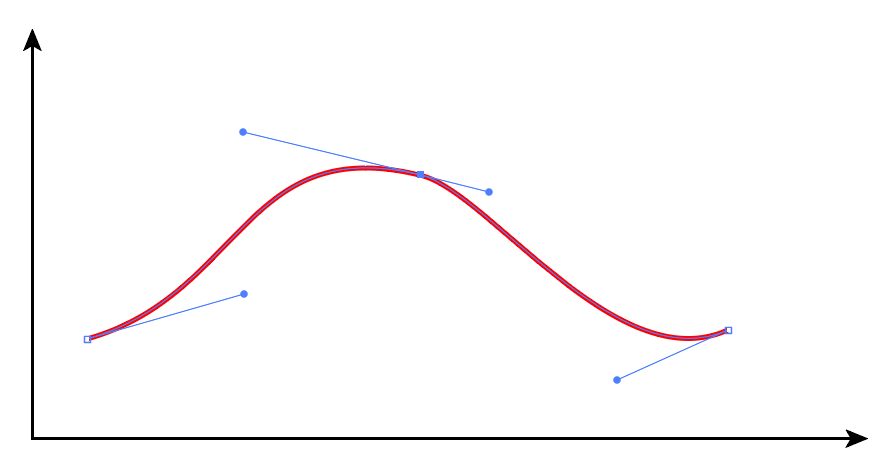
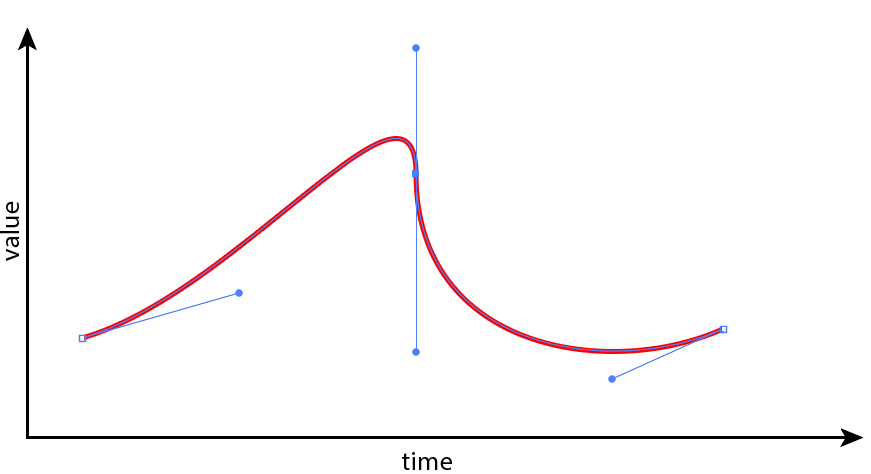
However, the glTF specification is associating the in- and out-tangents with the same timestamp as the vertex between them. In a traditional curve, this would represent a vertical section of the graph. Obviously that is incorrect, since the keyframe graph represents value per time, and thus a vertical line graph would represent an ambiguous situation where there are many possible values for the same time.

My question is, what do these tangent values represent, in a traditional cubic Bézier spline? Or, more to the point:

Given the tangent values per keyframe, how can I construct cubic Bézier control points as part of a Bézier curve that will accurately visually depict the time/value graph that occurs due to the equation specified?

Update: I've created a Desmos graph that performs the above calculation, to experiment with the curve. I've come to believe that the tangent values do not appear to represent actual target values. Instead, they are treated like offsets to the keyframe values on each side:

• The curve starts at v_k and trends towards v_k b_k
• The curve ends at v_{k 1} and on the way trends towards v_{k 1} - a_{k 1}

Experimentally sketching cubic Bézier to fit over the Desmos curve shows that the time values of the control points should always be at t=1/3 and t=2/3 (as guessed at by this answer to a related question).

I'm still looking for the formula that incorporates t_d, but I'm close. It looks like the control points are exactly at (0.333, v_k b_k) and (0.666, v_{k 1} - a_{k 1}) when t_d = 3, but that may just be a coincidence in my experiments.

CodePudding user response：

The glTF Tutorial on Animations offers this further explanation:

The input and output tangents are normalized vectors that will need to be scaled by the duration of the keyframe, we call that the deltaTime

deltaTime = nextTime - previousTime

In other words, a normalized incoming or outgoing direction has been encoded, but it does not contain any magnitude.

The tutorial goes on to offer this pseudocode implementation of the reference formula given in Appendix C of the glTF specification:

Point cubicSpline(previousPoint, previousTangent,
                  nextPoint, nextTangent, interpolationValue)
    t = interpolationValue
    t2 = t * t
    t3 = t2 * t
    
    return (2 * t3 - 3 * t2   1) * previousPoint  
           (t3 - 2 * t2   t) * previousTangent  
           (-2 * t3   3 * t2) * nextPoint  
           (t3 - t2) * nextTangent;

The above code can be treated as all "floats" (or doubles) when animating scalar values, or can be treated as 3D vectors for interpolating X, Y, and Z animations in one pass. The "interpolationValue" is a normalized zero-to-one timeline position between adjacent keyframes.

CodePudding user response：

My question is, what do these tangent values represent, in a traditional cubic Bézier spline?

They appear to be offsets to the keyframe values (positive offset for the out tangent, negative offset for the in tangent) placed a third of the way between the keyframes, and unscaled (dividied) by the amount of time between the keyframes.

I don't know why the following works, just that experimentally it produces the same results as plotting the equation from the specification. (I'll happily formally accept instead an answer that proves this to be correct through proper Math. :)

Given:

• t_k, t_{k 1}: the time for keyframes k and k 1
• v_k, v_{k 1}: the property value for keyframes k and k 1
• b_k: the out-tangent value for keyframe k
• a_{k 1}: the in-tangent value for keyframe k 1

We define:

• t_d3 = (t_{k 1} - t_k) / 3

And then we can compute the four cubic Bézier control points for that segment at the time/value points:

• a = (t_k, v_k)
• b = (t_k t_d3, v_k b_k × t_d3)
• c = (t_{k 1} - t_d3, v_{k 1} - a_{k 1} × t_d3)
• d = (t_{k 1}, v_{k 1})