I am following the code

I am not sure if there is a method to find the center of the white region directly, but if there is, that would be most helpful. My initial idea was to draw two perpendicular intersecting lines over the image to find the center -- perhaps by measuring the width and height of the region -- but I am not sure of how efficient this is, nor how to implement this.

Any method to be able to measure the center of the segmented region would be much appreciated. Thank you.

Here is the code I have to produce the segmented image (almost identical to the code in the link):

import keras, os, copy, pydicom, cv2, glob
import matplotlib.pyplot as plt
import numpy as np
import nibabel as nib
import scipy.ndimage
import pandas as pd
from skimage import filters
from math import *
from skimage import measure, morphology
from skimage.morphology import ball, binary_closing
from skimage.measure import label, regionprops
from functools import reduce
from scipy.linalg import norm

path = "filepath" #for me, the filepath is to a DICOM .dcm file

def load_scan(path):
    slices = [pydicom.dcmread(path   '/'   s) for s in               
              os.listdir(path)]
    slices = [s for s in slices if 'SliceLocation' in s]
    slices.sort(key = lambda x: int(x.InstanceNumber))
    try:
        slice_thickness = np.abs(slices[0].ImagePositionPatient[2] -   
                          slices[1].ImagePositionPatient[2])
    except:
        slice_thickness = np.abs(slices[0].SliceLocation - 
                      slices[1].SliceLocation)
    for s in slices:
        s.SliceThickness = slice_thickness
    return slices

def get_pixels_hu(scans):
    image = np.stack([s.pixel_array for s in scans])
    image = image.astype(np.int16)
    # Set outside-of-scan pixels to 0
    # The intercept is usually -1024, so air is approximately 0
    image[image == -2000] = 0
    
    # Convert to Hounsfield units (HU)
    intercept = scans[0].RescaleIntercept
    slope = scans[0].RescaleSlope
    
    if slope != 1:
        image = slope * image.astype(np.float64)
        image = image.astype(np.int16)
        
    image  = np.int16(intercept)
    
    return np.array(image, dtype=np.int16)

patient_dicom = load_scan(path)
patient_pixels = get_pixels_hu(patient_dicom)

def largest_label_volume(im, bg=-1):
    vals, counts = np.unique(im, return_counts=True)
    counts = counts[vals != bg]
    vals = vals[vals != bg]
    if len(counts) > 0:
        return vals[np.argmax(counts)]
    else:
        return None
    
def segment_lung_mask(image, fill_lung_structures=True):
    # not actually binary, but 1 and 2. 
    # 0 is treated as background, which we do not want
    binary_image = np.array(image >= -800, dtype = np.int8)   1
    labels = measure.label(binary_image)
 
    # Pick the pixel in the very corner to determine which label is air.
    # Improvement: Pick multiple background labels from around the patient
    # More resistant to “trays” on which the patient lays cutting the air around the person in half 
    background_label = labels[0,0,0]
 
    # Fill the air around the person
    binary_image[background_label == labels] = 1
 
    # Method of filling the lung structures (that is superior to 
    # something like morphological closing)
    if fill_lung_structures:
        # For every slice we determine the largest solid structure
        for i, axial_slice in enumerate(binary_image):
            axial_slice = axial_slice - 1
            labeling = measure.label(axial_slice)
            l_max = largest_label_volume(labeling, bg=0)
 
            if l_max is not None: #This slice contains some lung
                binary_image[i][labeling != l_max] = 1
            
    binary_image -= 1 #Make the image actual binary
    binary_image = 1-binary_image # Invert it, lungs are now 1
 
    # Remove other air pockets inside body
    labels = measure.label(binary_image, background=0)
    l_max = largest_label_volume(labels, bg=0)
    if l_max is not None: # There are air pockets
        binary_image[labels != l_max] = 0
 
    return binary_image

# get masks 
segmented_lungs = segment_lung_mask(patient_pixels,    
                    fill_lung_structures = False)
segmented_lungs_fill = segment_lung_mask(patient_pixels,     
                    fill_lung_structures = True)
#internal_structures = segmented_lungs_fill - segmented_lungs

# isolate lung from chest
copied_pixels = copy.deepcopy(patient_pixels)
for i, mask in enumerate(segmented_lungs_fill): 
    get_high_vals = mask == 0
    copied_pixels[i][get_high_vals] = 0
seg_lung_pixels = copied_pixels

# sanity check
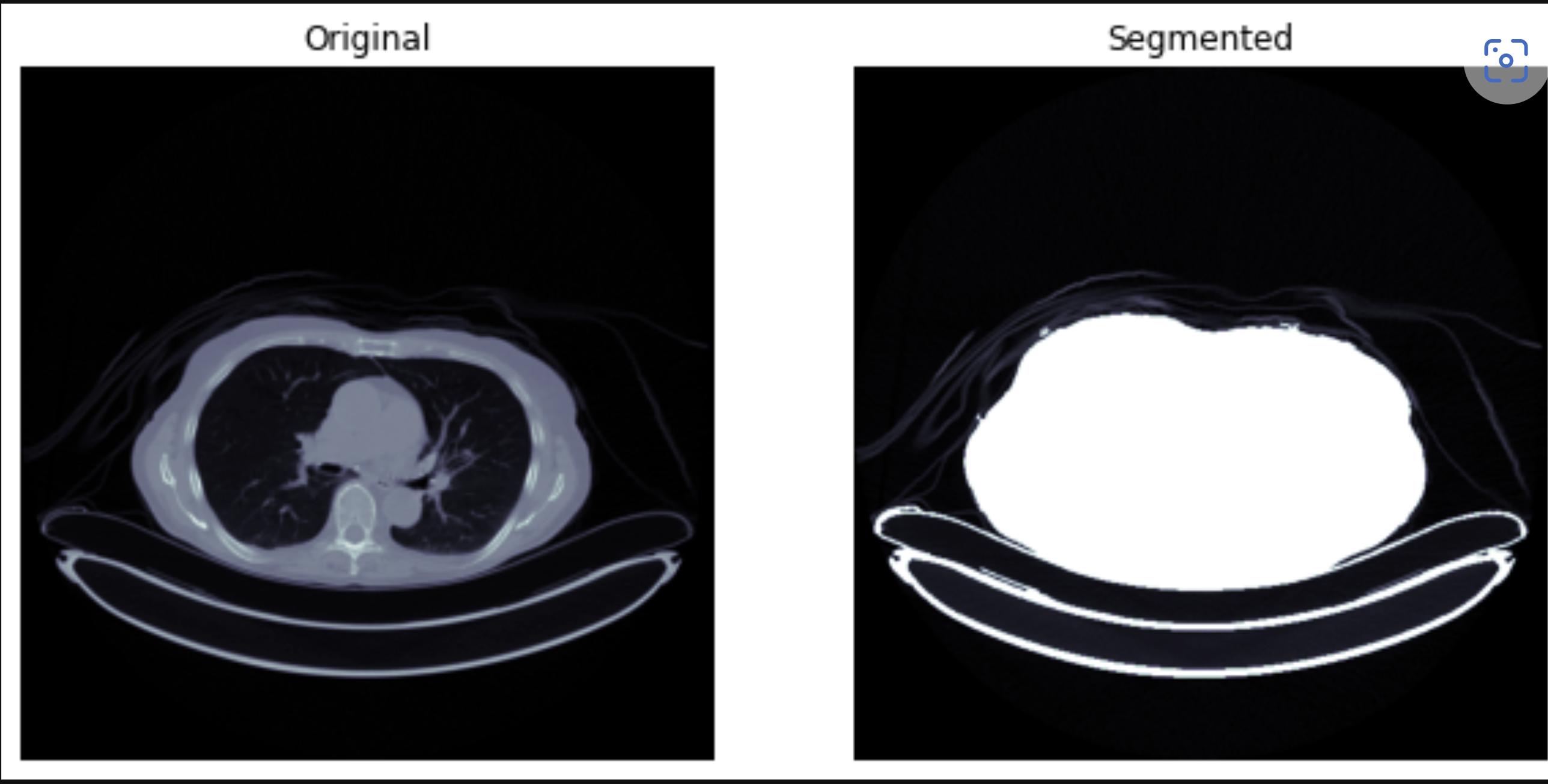
f, ax = plt.subplots(1,2, figsize=(10,6))
ax[0].imshow(patient_pixels[60], cmap=plt.cm.bone)
ax[0].axis(False)
ax[0].set_title('Original')
ax[1].imshow(seg_lung_pixels[60], cmap=plt.cm.bone)
ax[1].axis(False)
ax[1].set_title('Segmented')
plt.show()

CodePudding user response：

# Assume binary_mask is a 2D numpy array with dtype bool
centroid = np.mean(np.argwhere(binary_mask),axis=0)
centroid_x, centroid_y = int(centroid[1]), int(centroid[0])

CodePudding user response：

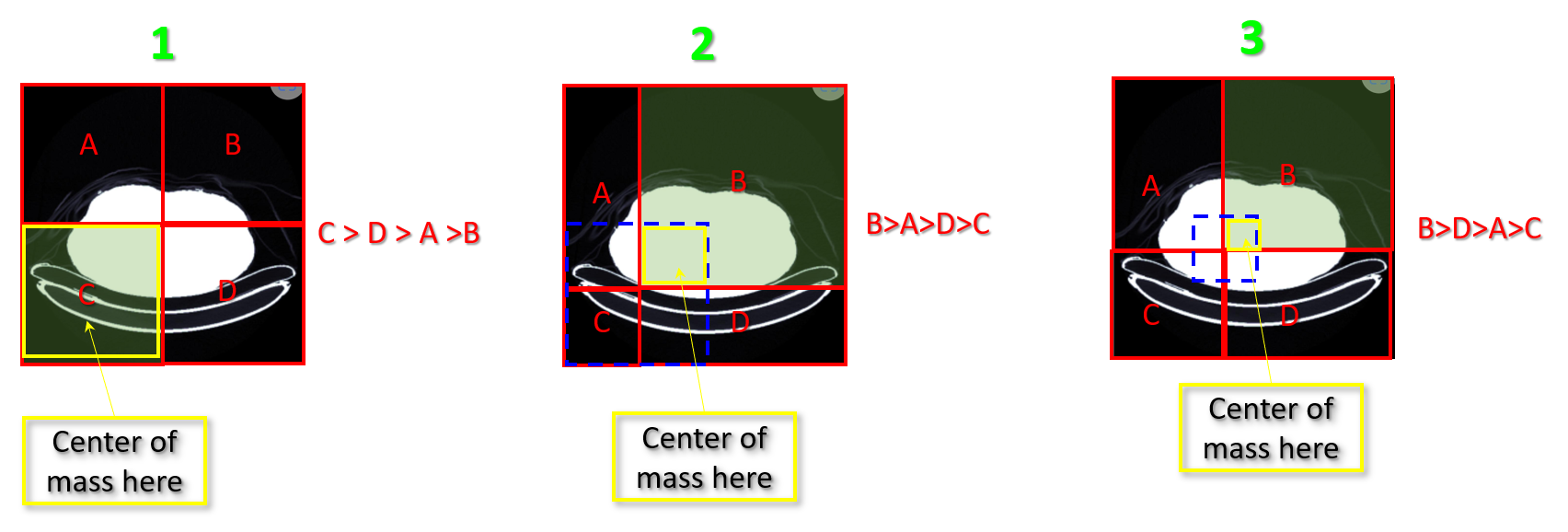
• split the image into 4 equal rectangles (step 1)
• Count the white pixels inside each rectangle A,B,C,D
• Find the rectangle with the most white pixels, the center of mass point will be inside this rectangle (in the example above it is C)
• take the center point of the winner rectangle (C in step 1) and find the center point of it
• adjust the four rectangles depending on this center point (Step 2)
• Count the white pixels inside each new rectangle A,B,C,D
• Find the rectangle with the most white pixels, the center of mass point will be inside this rectangle (in the example above it is B)
• the intersected rectangle of the winner from step 1 and the winner from step 2 has the center of mass point inside it.
• ...
• ...
• ... etc
• Until you find the point which have 4 rectangle with the same weight (white pixels count) and this is the center of mass

It is like trying to balance an object on your finger and keep adjusting until it is totally balanced.