Map an angle to a range of 2 other angles-CodePudding

I hope this will make sense

I'm trying to write a function that given an angle, computes a 0.0 to 1.0 range that represents an arc angle in a circle where the start (where 0.0 maps to on the circle) and end (where 1.0 maps to on the circle) are arbitrary.

start and end can be anything from -π to 4π, but their difference will always be <= 2π.

The line above is important!!! Let's say you want to map the entire circle. start = -π, end = π works but we want to support ANY mapping So for example from 6 o'clock clockwise back to 6 o'clock we can NOT specify with start = π/2, end = π/2 But we can specify it with start = π/2, end = π * 2.5.

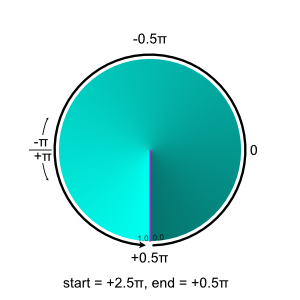
Similarly we can go the other way, start = π * 2.5, end = π * 0.5

Notice the direction of the mapping has changed. The point is I'm trying to handle any mapping and you need way to specify "around the circle" so a start of N and an end of N 2π = clockwise from N around the entire circle, where as start of N and end of N - 2π = counter-clockwise from N around the entire circle.

The part I'm stumbling on is the discontinuity between -π/ π and converting from my angle to my 0.0 to 1.0 value.

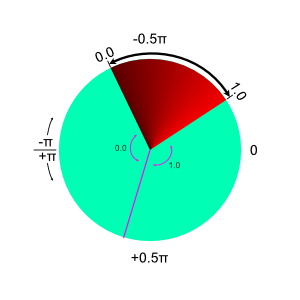
Let's call 0.0 start, and 1.0 end. In the first diagram above, start is at around -0.6π and end is around -0.2π. In this case it's kind of easy

result = (angle - startAngle) / (endAngle - startAngle)

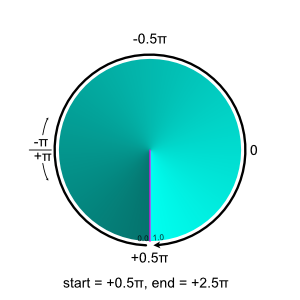
It fails if my arc is large but want to set where 0.0 and 1.0 are. For example if I set start to 0.5π (down) and I set end to 2.5π so the entire circle where 0.0 is down (6 o'clock), 0.25 is right (9 o'clock), 0.5 is up (12 o'clock), 0.7 is right (3 o'clock) and 1.0 is back down (6 o'clock)

Further, for the angles outside of the red range, I want half of it clamp to 0 and the other half to 1.0. If I just did

result = clamp(results, 0, 1)

Looking at the circle as a clock, i'd get 0 from 9:00 to 11:00 (small area) where as I'd get 1 from 2:00 to 9:00 (large). Where as what I want is 0 from 7:00 to 11:00 and 1 from 2:00 to 7:00 (areas are equal sizes)

I feel like I'm having to write lots of special cases and I keep running into bugs and so I thought I'd ask if there is a simple way to do this. In other words, write the function

result = mapAngleToArc(angle, startAngleInRadians, endAngleInRadians);

I don't really want to show code because I don't want to lead people down a bad path. I expect there's some simple math involving dot products that just figures this out without having to check if endAngleInRadians is less than startAngleInRadians.... or maybe there isn't.

Some people are claiming just adding 2π here or there solves everything. Well, where do I add it?. Maybe try answering the question directly instead if just giving vague hints.

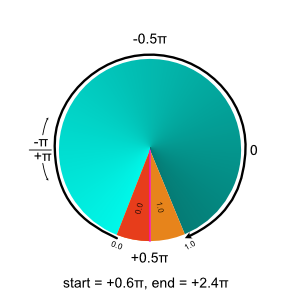
Here's another example:

Where do I add 2π? The inputs

angle = -π <->  2π
start = π*0.6
end = π*2.4

Expected results

-angle-	-result-
0.55π	0.0
0.6π	0.0
-0.5π	0.5
0.24π	1.0
0.245π	1.0

Where do I add or mod by 2π to get these results?

Note: I don't really care which language but if I have to pick one I'd pick JavaScript if only because it's each to make a live example in a snippet but I suspect there are more C programmers with experience with this type of problem. Anyway, here's a live example to play with

const ctx = document.querySelector('canvas').getContext('2d');
const logElem = document.querySelector('pre');

function drawCircle(ctx, cx, cy, start, end) {
  ctx.beginPath();
  ctx.arc(cx, cy, 70, 0, Math.PI * 2);
  ctx.fillStyle = 'cyan';
  ctx.fill();

  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 70, start, end);
  ctx.fillStyle = 'red';
  ctx.fill();

  const range = end - start;
  const unRange = Math.PI * 2 - range;

  // draw 0.0 area
  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 60, start - unRange / 2, start);
  ctx.fillStyle = 'pink';
  ctx.fill();

  // draw 1.0 area
  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 60, end, end   unRange / 2);
  ctx.fillStyle = 'orange';
  ctx.fill();

}

function drawPoint(ctx, x, y) {  
  ctx.beginPath();
  ctx.arc(x, y, 2, 0, Math.PI * 2);
  ctx.fillStyle = 'black';
  ctx.fill();
}

function drawAngle(ctx, px, py, cx, cy) {
  ctx.save();
  ctx.translate(cx, cy);
  const dx = s.pointX - circleX;
  const dy = s.pointY - circleY;
  const angle = Math.atan2(dy, dx);
  ctx.rotate(angle);
  ctx.beginPath();
  ctx.moveTo(0, 0);
  ctx.lineTo(65, 0);
  ctx.strokeStyle = 'yellow'
  ctx.stroke();
  ctx.restore();
}

const circleX = 150;
const circleY = 75;
const s = {
  start: Math.PI * -0.7,
  end: Math.PI * -0.1,
  pointX: 160,
  pointY: 40,
};


function radToDeg(rad) {
  return (rad * 180 / Math.PI).toFixed(1);
}

function clamp(v, min, max) {
  return Math.min(max, Math.max(min, v));
}

function draw() {
  ctx.clearRect(0, 0, ctx.canvas.width, ctx.canvas.height);
  drawCircle(ctx, circleX, circleY, s.start, s.end);
  drawAngle(ctx, s.pointX, s.pointY, circleX, circleY);
  drawPoint(ctx, s.pointX, s.pointY);

  const dx = s.pointX - circleX;
  const dy = s.pointY - circleY;
  const angle = Math.atan2(dy, dx);
 
  const result = mapAngleToArc(angle, s.start, s.end);
      
  logElem.textContent = `\
 angle: ${angle.toFixed(3)} (${radToDeg(angle)})
result: ${result.toFixed(3)}
`;
}

function mapAngleToArc(angle, startAngle, endAngle) {
  const result = (angle - startAngle) / (endAngle - startAngle);
  return clamp(result, 0, 1);
}

const GUI = lil.GUI;

const gui = new GUI().onChange(draw);
gui.add(s, 'start', -Math.PI, Math.PI * 4);
gui.add(s, 'end', -Math.PI, Math.PI * 4);
draw();

function handleMove(e) {
  s.pointX = e.offsetX;
  s.pointY = e.offsetY;
  draw();
}

function handleUp() {
  window.removeEventListener('mousemove', handleMove);
  window.removeEventListener('mouseup', handleUp);
}

ctx.canvas.addEventListener('mousedown', e => {
  window.addEventListener('mousemove', handleMove);
  window.addEventListener('mouseup', handleUp);
  handleMove(e);
});

<canvas></canvas>
<pre></pre>
<p>
When in the pink area should return 0.0<br>
When in the orange area should return 1.0<br>
Along to red area should return 0.0 &lt;-&gt; 1.0<br>
Should work for any values of start and end as long a<br>
<code>Math.abs(end - start) <= Math.PI * 2</code>
</p>
<script src="https://cdn.jsdelivr.net/npm/[email protected]"></script>

// C   version

float clamp(float v, float min, float max) {
  return std::min(max, std::max(min, v));
}

float mapAngleToArg(float angle, float start, float end) {
  ASSERT(start > -M_PI && start < M_PI * 4);
  ASSERT(end > -M_PI && end < M_PI * 4);
  ASSERT(std::abs(end - start) <= M_PI * 2);

  float result = (angle - start) / (end - start);
  return clamp(result, 0.0f, 1.0f);
}

CodePudding user response：

It looks like you have muddled thinking about what your problem is, and as a result you've asked a very complicated question which has no easy answer.

So let's start with what you consider easy. As you said, "There is no ambiguity given a start=0.5π, end=2.5π. It's clear I want a range around the circle starting where 0.5π points and ending where 2.5π points." I agree with that.

But now you want to also handle tricky cases like start=0.9π, end=-0.9π. You want to make this mean the clockwise arc from 0.9π to 1.1π. But it could just as reasonably also mean the counterclockwise arc from 0.9π to -0.9π. Insisting that it should be clockwise means that your code has a lot of DWIM (Do What I Mean) magic. Which, as you've discovered, means piling on edge cases as what you mean is not what the code so far guesses you to mean. And once you've got it meaning what YOU think it should mean, you'll inevitably find it hard to explain to others. And when you do, you'll fin that THEY want it to mean something else!

But if you allow the counterclockwise interpretation, then all special cases disappear. Your problem boils down to adjusting start to be in the right range by adding the right multiple of 2π. Then doing the same thing to the end. And now the direction is the sign of end-start, and the size of the angle is likewise.

And now there is no magic, no edge cases, and no complications. It is easy to write, easy to explain, and easy to understand.

(Random note, you've reversed the normal conventions about angles. Normally positive radians means moving counterclockwise. I followed your diagram in my explanation. But if you want others to use it, I'd recommend switching to what is standard.)

CodePudding user response：

Well, here's what I ended up with

Basically compute the center between start and end, then rotate everything, start, end, angle so center is at 0 by subtracting center from everything. That means start and end are now on opposite sides of center and the negatives of each other and effectively the furthest anything can be from center is the opposite side.

function clamp(v, min, max) {
  return Math.min(max, Math.max(min, v));
}

function euclideanModulo(v, n) {
  return ((v % n)   n) % n;
}

function twoPiMod(v) {
  return euclideanModulo(v   Math.PI, Math.PI * 2) - Math.PI;
}

function mapAngleToArc(angle, start, end) {
  const center = (start   end) / 2;

  const centeredAngle = twoPiMod(angle - center);
  const centeredStart = twoPiMod(start - center);
  const newV = (centeredAngle - centeredStart) / (end - start);
  return clamp(newV, 0, 1);
}

const ctx = document.querySelector('canvas').getContext('2d');
const logElem = document.querySelector('pre');

function drawCircle(ctx, cx, cy, start, end) {
  ctx.beginPath();
  ctx.arc(cx, cy, 70, 0, Math.PI * 2);
  ctx.fillStyle = 'cyan';
  ctx.fill();

  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 70, start, end);
  ctx.fillStyle = 'red';
  ctx.fill();

  const range = end - start;
  const unRange = Math.PI * 2 - range;

  // draw 0.0 area
  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 60, start - unRange / 2, start);
  ctx.fillStyle = 'pink';
  ctx.fill();

  // draw 1.0 area
  ctx.beginPath();
  ctx.moveTo(cx, cy);
  ctx.arc(cx, cy, 60, end, end   unRange / 2);
  ctx.fillStyle = 'orange';
  ctx.fill();

}

function drawPoint(ctx, x, y) {  
  ctx.beginPath();
  ctx.arc(x, y, 2, 0, Math.PI * 2);
  ctx.fillStyle = 'black';
  ctx.fill();
}

function drawAngle(ctx, px, py, cx, cy) {
  ctx.save();
  ctx.translate(cx, cy);
  const dx = s.pointX - circleX;
  const dy = s.pointY - circleY;
  const angle = Math.atan2(dy, dx);
  ctx.rotate(angle);
  ctx.beginPath();
  ctx.moveTo(0, 0);
  ctx.lineTo(65, 0);
  ctx.strokeStyle = 'yellow'
  ctx.stroke();
  ctx.restore();
}

const circleX = 150;
const circleY = 75;
const s = {
  start: Math.PI * -0.7,
  end: Math.PI * -0.1,
  pointX: 160,
  pointY: 40,
};


function radToDeg(rad) {
  return (rad * 180 / Math.PI).toFixed(1);
}

function clamp(v, min, max) {
  return Math.min(max, Math.max(min, v));
}

function draw() {
  ctx.clearRect(0, 0, ctx.canvas.width, ctx.canvas.height);
  drawCircle(ctx, circleX, circleY, s.start, s.end);
  drawAngle(ctx, s.pointX, s.pointY, circleX, circleY);
  drawPoint(ctx, s.pointX, s.pointY);

  const dx = s.pointX - circleX;
  const dy = s.pointY - circleY;
  const angle = Math.atan2(dy, dx);
 
  const result = mapAngleToArc(angle, s.start, s.end);
  const bad = Math.abs(s.start - s.end) > Math.PI * 2;

  logElem.textContent = bad
      ? 'ERROR: Math.abs(start - end) > Math.PI * 2'
      : `\
 angle: ${angle.toFixed(3)} (${radToDeg(angle)})
result: ${result.toFixed(3)}
`;
}

function euclideanModulo(v, n) {
  return ((v % n)   n) % n;
}

function twoPiMod(v) {
  return euclideanModulo(v   Math.PI, Math.PI * 2) - Math.PI;
}

function mapAngleToArc(angle, start, end) {
  const center = (start   end) / 2;

  const centeredAngle = twoPiMod(angle - center);
  const centeredStart = twoPiMod(start - center);
  const newV = (centeredAngle - centeredStart) / (end - start);
  return clamp(newV, 0, 1);
}

const GUI = lil.GUI;

const gui = new GUI().onChange(draw);
gui.add(s, 'start', -Math.PI, Math.PI * 4);
gui.add(s, 'end', -Math.PI, Math.PI * 4);
draw();

function handleMove(e) {
  s.pointX = e.offsetX;
  s.pointY = e.offsetY;
  draw();
}

function handleUp() {
  window.removeEventListener('mousemove', handleMove);
  window.removeEventListener('mouseup', handleUp);
}

ctx.canvas.addEventListener('mousedown', e => {
  window.addEventListener('mousemove', handleMove);
  window.addEventListener('mouseup', handleUp);
  handleMove(e);
});

<canvas></canvas>
<pre></pre>
<p>
When in the pink area should return 0.0<br>
When in the orange area should return 1.0<br>
Along to red area should return 0.0 &lt;-&gt; 1.0<br>
Should work for any values of start and end as long a<br>
<code>Math.abs(end - start) <= Math.PI * 2</code>
</p>
<script src="https://cdn.jsdelivr.net/npm/[email protected]"></script>