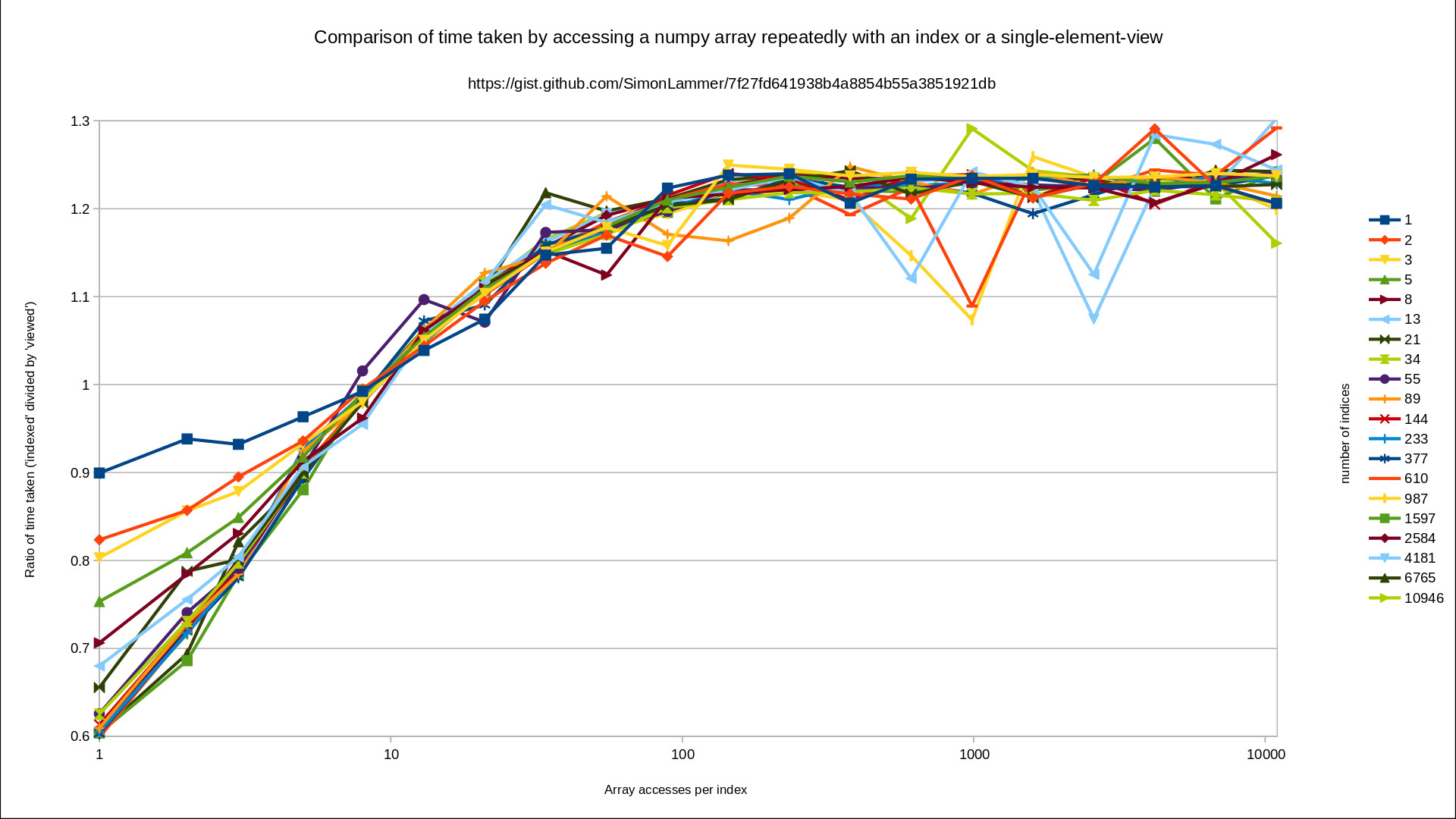
The data for this plot was created by timing the two aproaches (in python 3.10):
#!/bin/python3
# https://gist.github.com/SimonLammer/7f27fd641938b4a8854b55a3851921db
from datetime import datetime, timedelta
import numpy as np
import timeit
np.set_printoptions(linewidth=np.inf, formatter={'float': lambda x: format(x, '1.5E')})
def indexed(arr, indices, num_indices, accesses):
s = 0
for index in indices[:num_indices]:
for _ in range(accesses):
s = arr[index]
def viewed(arr, indices, num_indices, accesses):
s = 0
for index in indices[:num_indices]:
v = arr[index:index 1]
for _ in range(accesses):
s = v[0]
return s
N = 11_000 # Setting this higher doesn't seem to have significant effect
arr = np.random.randint(0, N, N)
indices = np.random.randint(0, N, N)
options = [1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946]
for num_indices in options:
for accesses in options:
print(f"{num_indices=}, {accesses=}")
for func in ['indexed', 'viewed']:
t = np.zeros(5)
end = datetime.now() timedelta(seconds=2.5)
i = 0
while i < 5 or datetime.now() < end:
t = timeit.repeat(f'{func}(arr, indices, num_indices, accesses)', number=1, globals=globals())
i = 1
t /= i
print(f" {func.rjust(7)}:", t, f"({i} runs)")
These observations are very counterintuitive to me.
Why is viewed faster than indexed (for more than 10 accesses per index)?
Edit 1:
- gist crossreference: https://gist.github.com/SimonLammer/7f27fd641938b4a8854b55a3851921db
- r/Numpy crossreference: https://www.reddit.com/r/Numpy/comments/wb4p12/why_is_repeated_numpy_array_access_faster_using_a/
CodePudding user response:
Since num_indices have not significant impact on the observed performance, we can simplify the problem by discarding this parameter (ie. set to 1). Since only large accesses matters, we can also simplify the problem by considering only a large value like 10946 for example. The use of index can also be simplified without affecting the benchmark. The same thing applies for the return statement. The simplified problem is now why we get this (reproduced on CPython 3.10.5):
import numpy as np
def indexed(arr, index):
s = 0
for _ in range(10946): s = arr[index]
def viewed(arr, index):
s = 0
v = arr[index:index 1]
for _ in range(10946): s = v[0]
N = 11_000
arr = np.random.randint(0, N, N)
indices = np.random.randint(0, N, N)
# mean ± std. dev. of 7 runs, 1000 loops each
%timeit indexed(arr, indices[0]) # 1.24 ms ± 22.3 µs per loop
%timeit viewed(arr, indices[0]) # 0.99 ms ± 4.34 µs per loop
Now, the source of the slowdown is pretty limited. It only has to do with arr[index] versus v[0]. It is also important to note that arr and v are basically of the same type meanwhile index and 0 are not of the same type. Indeed, index if of type np.int64 while 0 is a PyLong object. The thing is Numpy item types are much slower than builtin ones since the interpreter can use builtin functions on builtin types (meanwhile Numpy do many internal function calls and checks).
To fix the problem, you can just convert the Numpy type to a builtin one:
import numpy as np
def indexed(arr, index):
s = 0
nativeIndex = int(index) # <------------------------------
for _ in range(10946): s = arr[nativeIndex]
def viewed(arr, index):
s = 0
v = arr[index:index 1]
for _ in range(10946): s = v[0]
N = 11_000
arr = np.random.randint(0, N, N)
indices = np.random.randint(0, N, N)
# mean ± std. dev. of 7 runs, 1000 loops each
%timeit indexed(arr, indices[0]) # 981 µs ± 4.6 µs per loop
%timeit viewed(arr, indices[0]) # 989 µs ± 5.3 µs per loop
# The difference is smaller than the sum of the standard deviations
# so the gap is clearly not statistically significant anymore.
Besides, note that nearly all the time of the two functions is pure overhead. Numpy is not designed for doing scalar access, but optimized for vectorized ones. A naive expression like v[0] cause a LOT of work to be done by the processor: the expression needs to be interpreted, a new reference-counted object need to be allocated, several (internal) functions of Numpy needs to be called with many overheads (wrapping, dynamic type checking, internal iterator configuration). Low-level profilers reports dozens of function calls to be called and 250-300 cycles wasted for something that should take no more than 1 cycle of throughput on a modern x86 processor.
Related post: Why is np.sum(range(N)) very slow?
CodePudding user response:
Update: I can't replicate the timings of this answer anymore. Maybe I have done something in a setup step that changed these results; or they were just coincidence.
>>> arr = np.random.randint(0, 1000, 1000)
>>> i = 342
>>> def a3(i): return arr[i]
...
>>> def b3(i): return arr[342]
...
>>> def c3(i): return arr[0]
...
>>> t = timeit.repeat('a3(i)', globals=globals(), number=100000000); print(t, np.mean(t), np.median(t))
[17.449311104006483, 17.405843814995023, 17.91914719599299, 18.123263651999878, 18.04744581299019] 17.789002315996914 17.91914719599299
>>> t = timeit.repeat('b3(i)', globals=globals(), number=100000000); print(t, np.mean(t), np.median(t))
[17.55685576199903, 18.099313585989876, 18.032570399998804, 18.153590378991794, 17.628647994992207] 17.894195624394342 18.032570399998804
>>> t = timeit.repeat('c3(i)', globals=globals(), number=100000000); print(t, np.mean(t), np.median(t))
[17.762766532003297, 17.826293045000057, 17.821444382003392, 17.618322997994255, 17.488862683996558] 17.703537928199513 17.762766532003297
The timing difference seems to be caused by loading a variable vs. loading a constant.
import numpy as np
import dis
arr = np.random.randint(0, 1000, 1000)
def a3(i):
return arr[i]
def b3(i):
return arr[342]
def c3(i):
return arr[0]
The difference in these functions is just the way of indexing the array with i, 342 or 0.
>>> dis.dis(a3)
2 0 LOAD_GLOBAL 0 (arr)
2 LOAD_FAST 0 (i)
4 BINARY_SUBSCR
6 RETURN_VALUE
>>> dis.dis(b3)
2 0 LOAD_GLOBAL 0 (arr)
2 LOAD_CONST 1 (342)
4 BINARY_SUBSCR
6 RETURN_VALUE
>>> dis.dis(c3)
2 0 LOAD_GLOBAL 0 (arr)
2 LOAD_CONST 1 (0)
4 BINARY_SUBSCR
6 RETURN_VALUE
The variable index is (~8%) slower than a constant index, and a constant index 0 is (~5%) faster still. Accessing the array at index 0 (c3) is (~13%) faster than the variable index (a3).
>>> t = timeit.repeat('a3(i)', globals=globals(), number=10000000); print(t, np.mean(t), np.median(t))
[1.4897515250049764, 1.507482559987693, 1.5573357169923838, 1.581711255988921, 1.588776800010237] 1.5450115715968422 1.5573357169923838
>>> t = timeit.repeat('b3(i)', globals=globals(), number=10000000); print(t, np.mean(t), np.median(t))
[1.4514476449985523, 1.427873961001751, 1.4268056689907098, 1.4114146630017785, 1.442651974997716] 1.4320387825981016 1.427873961001751
>>> t = timeit.repeat('c3(i)', globals=globals(), number=10000000); print(t, np.mean(t), np.median(t))
[1.357518576012808, 1.3500928360008402, 1.3615708220022498, 1.376022889991873, 1.3813936790102161] 1.3653197606035974 1.3615708220022498
Thanks to u/jtclimb https://www.reddit.com/r/Numpy/comments/wb4p12/comment/ii7q53s/?utm_source=share&utm_medium=web2x&context=3
Edit 1: Using the setup parameter of timeit.repeat refutes this hypothesis.
>>> t=timeit.repeat('arr[i]', setup='import numpy as np; arr = np.random.randint(0,10000,1000000); i = 342', number=10000000); print(np.around(t, 5), np.mean(t), np.median(t))
[0.7697 0.76627 0.77007 0.76424 0.76788] 0.7676320286031114 0.7678760859998874
>>> t=timeit.repeat('arr[0]', setup='import numpy as np; arr = np.random.randint(0,10000,1000000); i = 342', number=10000000); print(np.around(t, 5), np.mean(t), np.median(t))
[0.76836 0.76629 0.76794 0.76619 0.7682 ] 0.7673966443951941 0.7679443680099212