Why numba with parallel=True is slower with this parallelizable for loop?-CodePudding

I am currently having difficulties understanding why the following code gets slower after including numba parallelization.

Here is the base code without specifying parallelization:

@njit('f8[:,::1](f8[:,::1], f8[:,::1], f8[:,::1])', fastmath=True)
def fun(A, B, C):

    n = A.shape[1]

    b00 = B[0,0]
    b02 = B[0,2]

    out = np.empty((n, 12))

    for i in range(n):

        ui = A[0,i]

        c1 = C[0,i]
        c2 = C[1,i]
        c3 = C[2,i]
        c4 = C[3,i]

        out[i, 0] = c1 * b00
        out[i, 1] = 0.
        out[i, 2] = c1 * (b02-ui)
        out[i, 3] = c2 * b00
        out[i, 4] = 0.
        out[i, 5] = c2 * (b02-ui)
        out[i, 6] = c3 * b00
        out[i, 7] = 0.
        out[i, 8] = c3 * (b02-ui)
        out[i, 9] = c4 * b00
        out[i, 10] = 0.
        out[i, 11] = c4 * (b02-ui)

    return out

and here is the parallelized version:

@njit('f8[:,::1](f8[:,::1], f8[:,::1], f8[:,::1])', fastmath=True, parallel=True)
def fun_parallel(A, B, C):

    n = A.shape[1]

    b00 = B[0,0]
    b02 = B[0,2]

    out = np.empty((n, 12))

    for i in prange(n):

        ui = A[0,i]

        c1 = C[0,i]
        c2 = C[1,i]
        c3 = C[2,i]
        c4 = C[3,i]

        out[i, 0] = c1 * b00
        out[i, 1] = 0.
        out[i, 2] = c1 * (b02-ui)
        out[i, 3] = c2 * b00
        out[i, 4] = 0.
        out[i, 5] = c2 * (b02-ui)
        out[i, 6] = c3 * b00
        out[i, 7] = 0.
        out[i, 8] = c3 * (b02-ui)
        out[i, 9] = c4 * b00
        out[i, 10] = 0.
        out[i, 11] = c4 * (b02-ui)

    return out

Measuring execution times with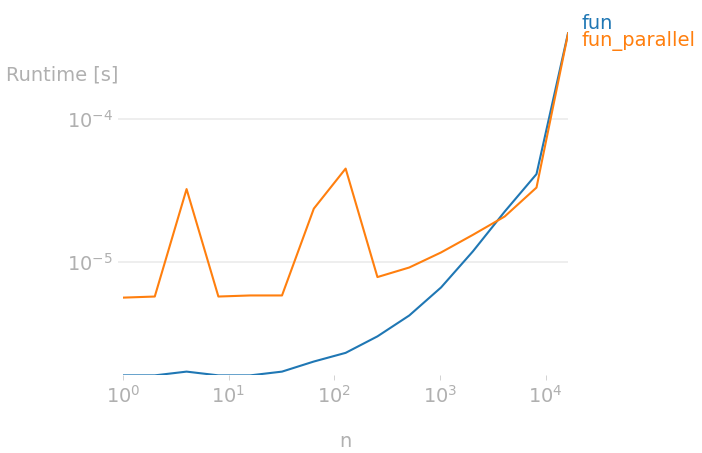

showing a noticeable increase in time execution with the parallelized version.

Any help on understanding why does this happen is much appreciated.

CodePudding user response：

TL;DR: parallelism only worth it for relatively-long compute-bound operations, clearly not for short memory-bound ones. Please consider merging algorithms so to make it more compute-bound.

When n is small, the overhead of creating threads or distributing the work (regarding the target parallel backend) is much bigger than the computation, as pointed out by Ali_Sh in the comments (see this past answer). Indeed, this is consistent with a constant overhead for small n values below 5e3 (though the time is unstable certainly because of OS syscalls, NUMA effects and non-deterministic synchronizations). The bigger the number of core, the bigger the overhead. Thus, parallelism can be beneficial on some machines (like my PC with 6 cores when n > 1e3). Reducing the number of thread should help a bit.

When n is big, using multiple threads do not provide a big speed-up because the operation is memory bound. Indeed, the RAM is shared between cores and few cores are generally enough to saturate it (if not 1 core on some PC). On my PC designed for reaching a high RAM throughput, 2 cores of my i5-9600KF processor are able to saturate the RAM with a throughput close to 40 GiB/s. Note that writing data in newly-created large array is not very efficient in Numba/Numpy. This is because the OS needs to do page-faults (generally during the first-touch, or during the np.empty on few system). One can pre-allocate the output array once so to avoid page-faults being done once again for each function call (assuming you can reuse the array). In addition, the write-allocate cache policy cause data to be read from memory so to write it which just waste half the memory bandwidth. there is no way to make that faster in Numba yet (there is an open issue on this). C/C codes can speed this up using non-temporal instructions on x86-64 platforms.

When n is sufficiently big for the parallel overhead to be relatively small and the computation is done in the CPU cache, using multiple thread can significantly help. That being said, this is a close window and this is probably what happen on your machine for 5e3 < n < 1e4.

Memory has been slow for few decades and it tends to be even slower than CPUs over time. This effect, called the "memory wall", was conjectured several decades ago and has been confirmed to be true so far. Thus, it is not expected for memory-bound codes to scale well any time soon (quite the opposite in fact). The only way to overcome this problem is to avoid operating on big buffers: data should be computed on the fly and using CPU caches as much as possible (especially the L1/L2 if possible). One should also prefer compute-bound algorithms over memory-bound one (for a similar amount of work). Recomputing data rather than pre-computing large buffers can be faster if the amount of computation is small.