What does time complexity actually mean?-CodePudding

I got the task of showing the time taken by the merge sort algorithm theoretically ( n log(n) ) and practically (by program) on a graph by using different values of n and time taken.

In the program, I'm printing the time difference between before calling the function and after the end of the function in microseconds I want to know what dose n log(n) means.

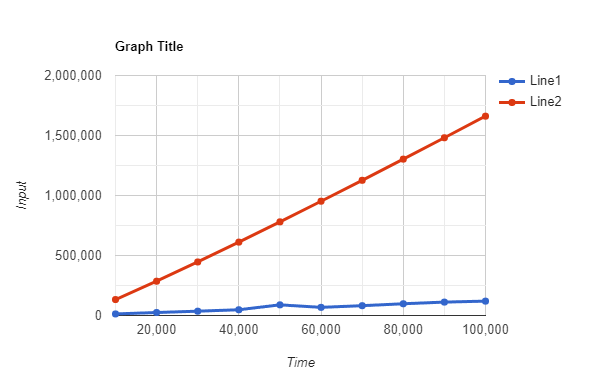
I tryed with this values: Number of values: 10000 20000 30000 40000 50000 60000 70000 80000 90000 100000

program time in micro second: 12964 24961 35905 47870 88764 67848 81782 97739 111702 119682

time using n log n formula: 132877 285754 446180 611508 780482 952360 1.12665e 006 1.30302e 006 1.48119e 006 1.66096e 006

code:

auto start = std::chrono::high_resolution_clock::now();
mergeSort(arr, 0, n - 1);
auto elapsed = std::chrono::high_resolution_clock::now() - start;
long long microseconds = std::chrono::duration_cast<std::chrono::microseconds>(elapsed).count();
cout << microseconds << " ";

Graph i got: Graph

CodePudding user response：

What time complexity actually means?

I interpret your question in the following way:

Why is the actual time needed by the program not K*n*log(n) microseconds?

The answer is: Because on modern computers, the same step (such as comparing two numbers) does not need the same time if it is executed multiple times.

If you look at the time needed for 50.000 and 60.000 numbers, you can see, that the 50.000 numbers even needed more time than the 60.000 numbers.

The reason might be some interrupt that occurred while the 50.000 numbers were sorted; I assume that you'll get a time between the 40.000 numbers and the 60.000 numbers if you run your program a second time.

In other words: External influences (like interrupts) have more impact on the time needed by your program than the program itself.

I got the task of showing the time taken by the merge sort algorithm theoretically (n log(n)) and practically (by program) on a graph by using different values of n and time taken.

I'd take a number of elements to be sorted that takes about one second. Let's say sorting 3 Million numbers takes one second; then I would sort 3, 6, 9, 12 ... and 30 Million numbers and measure the time.

This reduces the influence of interrupts etc. on the measurement. However, you'll still have some effect of the memory cache in this case.

You can use your existing measurements (especially the 50.000 and the 60.000) to show that for a small number of elements to be sorted, there are other factors that influence the run time.

CodePudding user response：

Note that a graph of y = x log(x) is surprisingly close to a straight line.

This is because the gradient at any point x is 1 log(x), which is a slowly growing function of x.

In other words, it's difficult within the bounds of experimental error to distinguish between O(N) and O(N log N).

The fact that the blue line is pretty straight is a reasonable verification that the algorithm is not O(N * N), but really without better statistical analysis and program control set-up, one can't say much else.

The difference between the red and blue line is down to "big O" not concerning itself with proportionality constants and other coefficients.

CodePudding user response：

The time complexity is the time a program takes to execute, as a function of the problem size.

The problem size is usually expressed as the number of input elements, but some other measures can sometimes be used (e.g. algorithms on matrices of size NxN can be rated in terms of N instead of N²).

The time can effectively be measured in units of time (seconds), but is often assessed by just counting the number of atomic operations of some kind performed (e.g. the number of comparisons, of array accesses...)

In fact, for theoretical studies, the exact time is not a relevant information because it is not "portable": it strongly depends on the performance of the computer used and also on implementation details.

This is why algorithmicians do not really care about exact figures, but rather on how the time varies with increasing problem sizes. This leads to the concept of asymptotic complexity, which measures the running time to an unknown factor, and for mathematical convenience, an approximation of the running time is often used, to make the computations tractable.

If you study the complexity by pure benchmarking (timing), you can obtain experimental points, which you could call empirical complexity. But some statistical rigor should be applied.

(Some of the other answers do merge the concepts of complexity and asymptotic complexity, but this is not correct.)

In this discussion of complexity, you can replace time by space and you study the memory footprint of the program.

CodePudding user response：

Time complexity has nothing to do with actual time. It's just a way that helps us to compare different algorithms - which algorithm will run faster.

For example - In case of sorting: we have bubble sort having time-complexity as O(n^2) and merge sort having time-complexity as O(N log(N)). So, with the help of time-complexity we can say that merge-sort is much better than bubble sort for sorting things.

Big-O notations was created so that we can have generalized way of comparing speed of different algorithms, a way which is not machine dependent.