I'm trying to find minimum in array which has this kind of structure in general:

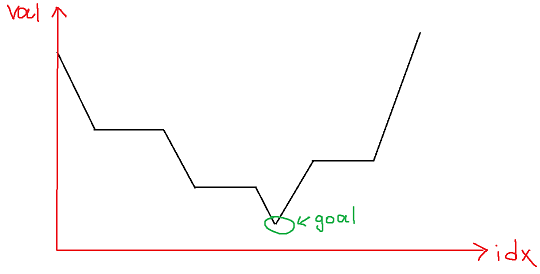
Array consists of non-negative integers [0; 1e5-1]. It may contain any number of such steps, be sorted or just a constant. I want to find it in O(logn) thats why I'm using binary search. This code handle all cases except cases there is any plateau:

size_t left = 0, right = arr.size() - 1;
while (left < right) {
    const size_t mid = left   (right - left) / 2;
    if ((mid == 0 || arr[mid] < arr[mid - 1]) && (mid   1 == size || arr[mid] < arr[mid   1])) {
        return mid;
    }
    if (arr[mid] > arr[mid   1] || arr[mid] > arr[right]) {
        left = mid   1;
    }
    else {
        right = mid;
    }
}
return left;

Example of bad input: [4, 3, 3, 2, 1, 2].

Unfortenatly, I'm out of ideas how to fix this cases. Maybe it's even impossible. Thank you in advance.

CodePudding user response：

I am afraid it is not possible to do in log n time in general.

1. Assume an array of n elements equal to 1 and a single element of 0.
2. Your problem now reduces into finding that 0 element.
3. By "visiting" (=indexing) any member 1 you gain no knowledge about position of 0 - making the search order irrelevant.
4. Therefore you have to visit every element to find where the 0 is.

If you really want, I think the following algorithm should be roughly O(log n #elements-on-plateaus)

1. Set left, right as for binary search
2. Compute middle.
3. Go left from middle until:
   • If you find a decrease, set right=pos where pos is the decreased element and go 4.
   • If you find an increase, set left=pos where pos is the increased element and go 4.
   • If you reach left position, go right from middle instead and do the analogous actions.
     • [X] If you reach right too, you are on a plateau and range [left,right] are the minimal elements of the array.
4. Repeat until you hit [X].