How to find all the combinations of variables (between 2 threshold values) that make an equation hol-CodePudding

Given the equation: 10 = 2x 3y 2z, I want to find all the combination of x, y and z between 2 thresholds (e.g. -100 and 100) that make the equation hold true.

So far, I have tried the following with no success (please see the comments):

set.seed(333)

result = 10

# sample random values from uniform distribution
x = runif(100, -100, 100)
y = runif(100, -100, 100)
z = runif(100, -100, 100)

# store the vectors in a single dataframe
df = data.frame(x, y, z)

# find all the combinations of x, y and z
expanded = expand.grid(df)

# calculation with all the combinations
expanded$result = ((expanded$x * 2)   (expanded$y * 3)   (expanded$z * 5)) == result

# show the data where result is 10
expanded[expanded$result, ]

[1] x      y      z      result
<0 rows> (or 0-length row.names)

How would I achieve this?

CodePudding user response：

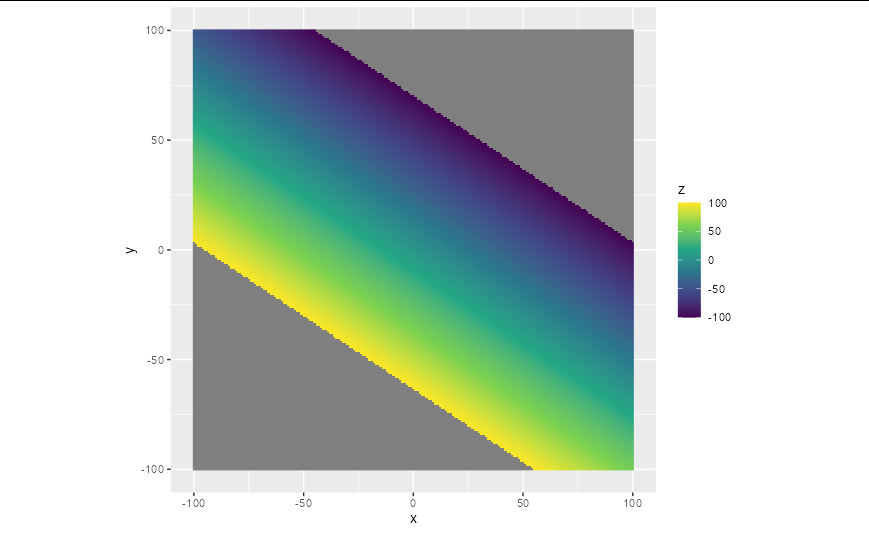
A linear equation of three variables can be thought of as a plane in 3D space. Solving your equation for z we have:

z = 5 - x - 1.5 * y

So we can at least see what the solution looks like. Let's examine all the valid integer values of x and y:

df <- expand.grid(x = seq(-100, 100), y = seq(-100, 100))

We can then get the corresponding values of z:

df$z <- 5 - df$x - 1.5 * df$y

But we need to disallow any values of z below -100 or above 100:

df$z[abs(df$z) > 100]  <- NA

And we can plot the resultant plane with the z value shown as a fill color:

ggplot(df, aes(x, y, fill = z))  
  geom_raster()  
  scale_fill_viridis_c()  
  coord_equal()

These at a glance, are all 25,184 integer solutions of your equation with the given constraints (as others have pointed out, there are of course an infinite number of non-integer solutions), and it's a reasonable approximation of the whole system. You can see all these combinations with

df[!is.na(df$z),]

CodePudding user response：

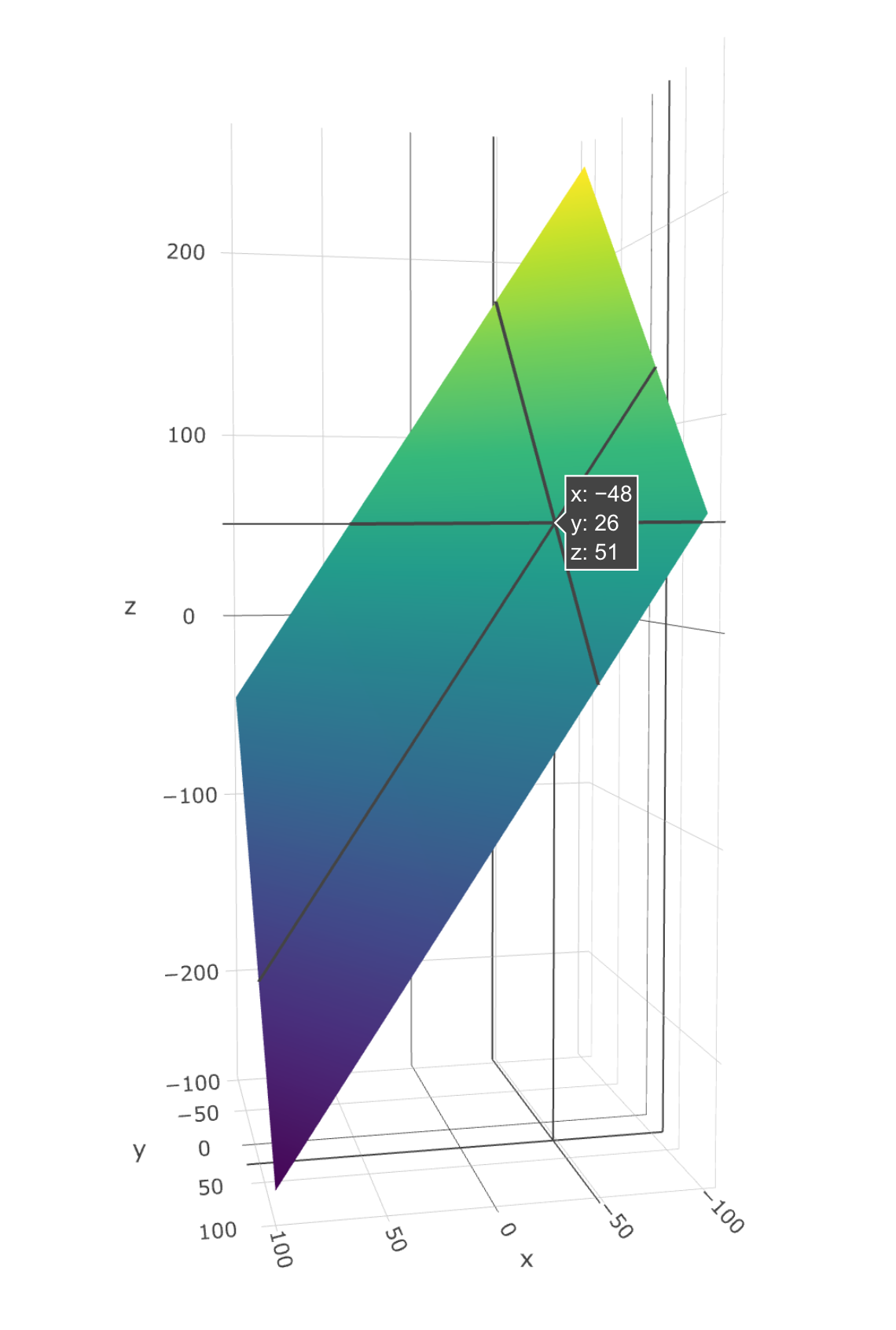
As multiple commenters have noted, your equation 10 = 2x 3y 2z forms a plane of possible values.

Consider this:

library(plotly)
myfunc <- \(x,y)5-x-(3/2 * y)
y <- x <- seq(-100,100,1)
z <- outer(x, y, myfunc)
plot_ly(x = x, y = y, z = z) %>%
   add_surface()

As you can see, given unlimited precision, there are an infinite number of points on that plane.