I am trying to simulate high dimension multivariate normal data in R with n = 100, and p = 400 (two different groups of variables with some correlations). Below are my codes:

## load library MASS
library(MASS)

## sample size set to n = 100
sample_size <- 100      

## I try to simulate two different groups of variables for each with 200 variables                  
sample_meanvector <- c(runif(200,0,1), runif(200,6,8))

## covariance matrix, some variables set to be correlated
sample_covariance_matrix <- matrix(NA, nrow = 400, ncol = 400)
diag(sample_covariance_matrix) <- 1
set.seed(666)
sample_covariance_matrix[lower.tri(sample_covariance_matrix)] <- runif(79800, 0.00001, 0.2)
sample_covariance_matrix[lower.tri(sample_covariance_matrix)][sample(1:79800, 10000)] <- runif(10000, 0.6, 0.9)

## make the matrix symmetric
sample_covariance_matrix[upper.tri(sample_covariance_matrix)]<-t(sample_covariance_matrix)[upper.tri(sample_covariance_matrix)]

## create multivariate normal distribution
sample_distribution <- mvrnorm(n = sample_size,
                               mu = sample_meanvector,
                               Sigma = sample_covariance_matrix)

However, every time I run this mvrnorm function, I got the error:

Error in mvrnorm(n = sample_size, mu = sample_meanvector, Sigma = sample_covariance_matrix) : 'Sigma' is not positive definite

I have two questions:

1. Why do I have this error?
2. How can I edit my codes to simulate the high dimension multivariate normal data following my idea mentioned above?

Thanks much!

CodePudding user response：

Here is an approach that can generate a highly correlated matrix :

library(MASS)
library(Matrix)

sample_size <- 100      
sample_meanvector <- c(runif(200,0,1), runif(200,6,8))
sample_covariance_matrix <- matrix(NA, nrow = 400, ncol = 400)
diag(sample_covariance_matrix) <- 1
set.seed(666)

mat_Sim <- matrix(data = NA, nrow = 400, ncol = 400)
U <- runif(n = 400) * 0.5

for(i in 1 : 400)
{
  if(i <= 350)
  {
    U_Star <- pmin(U   0.25 * runif(n = 400), 0.99999)
    
  }else
  {
    U_Star <- pmin(pmax(U   sample(c(-1, 1), size = 400, replace = TRUE) * runif(n = 400), 0.00001), 0.99999)
  }
  
  mat_Sim[, i] <- qnorm(U_Star)  
}

cor_Mat <- cor(mat_Sim)
sample_covariance_matrix <- cor_Mat * 200

## create multivariate normal distribution
sample_distribution <- mvrnorm(n = sample_size,
                               mu = sample_meanvector,
                               Sigma = sample_covariance_matrix)

image(cor_Mat)

with 7 / 8 of the matrix correlated between 0.6 and 0.8 and 1 / 8 of the matrix correlated between 0 and 0.3.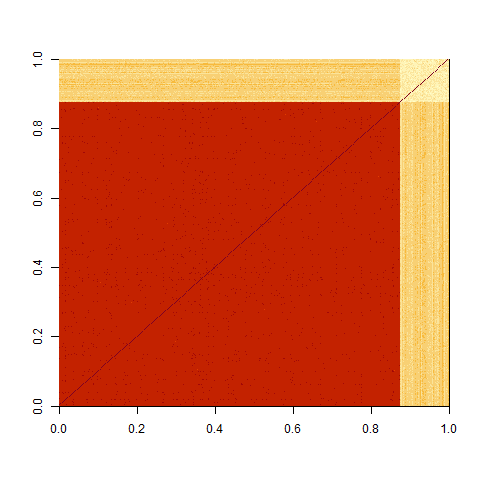

CodePudding user response：

You can consider the following code :

library(MASS)
library(Matrix)

sample_size <- 100      
sample_meanvector <- c(runif(200,0,1), runif(200,6,8))
sample_covariance_matrix <- matrix(NA, nrow = 400, ncol = 400)
diag(sample_covariance_matrix) <- 1
set.seed(666)
sample_covariance_matrix[lower.tri(sample_covariance_matrix)] <- runif(79800, 0.00001, 0.2)
sample_covariance_matrix[lower.tri(sample_covariance_matrix)][sample(1:79800, 10000)] <- runif(10000, 0.6, 0.9)
sample_covariance_matrix[upper.tri(sample_covariance_matrix)]<-t(sample_covariance_matrix)[upper.tri(sample_covariance_matrix)]
sample_covariance_matrix_Near_PD <- nearPD(sample_covariance_matrix)$mat


## create multivariate normal distribution
sample_distribution <- mvrnorm(n = sample_size,
                               mu = sample_meanvector,
                               Sigma = sample_covariance_matrix_Near_PD)