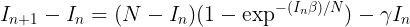Optimization problem for S-I-S model using python-CodePudding

I have a susceptible-infectious-susceptible model,

to which I've written the following python code,

def SIS(I0, beta, gamma, N=2000):
    f1 = N - I0

    f2 = -beta * I0
    f2 /= N
    f2 = 1 - exp(f2)

    f3 = gamma * I0

    return (f1 * f2) - f3   I0

And I'm solving it using the following code,

I0, beta, gamma, N = 10, 0.2, 0.25, 2000

t = np.linspace(0, 100, 101)

inf = [I0]

for i in t[:-1]:
    inf.append(SIS(inf[-1], beta, gamma))

This part is fine. I'm having trouble finding the double derivative 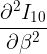and optimizing it for the value of the beta parameter. The problem is that the beta is not given and since that parameter is within the exponential function, it doesn't make sense to me to be able to get to the 10th value of the infectious parameter and then equate it to 0 to solve. I'm only given 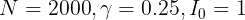for this particular problem.

If someone can guide me in the correct direction, that'd be a great help.

CodePudding user response：

You can use finite differences to approximate the derivate. An example for the second derivative:

h = 0.0001
t = 10
I_left   = solve(I0, t, beta-h, gamma, N)
I_right  = solve(I0, t, beta h, gamma, N)
I_center = solve(I0, t, beta, gamma, N)

d2I_dB2 = (I_right - I_center   I_left) / h**2

where solve solves the recurrence up to t.