Get a vector that is rotated towards a point that is perpendicular to a normal vector-CodePudding

I want to calculate a vector that is perpendicular to a normal vector of a plane, and if you are looking at the plane top down you will see the resulting vector pointing towards a point.

Example Image:

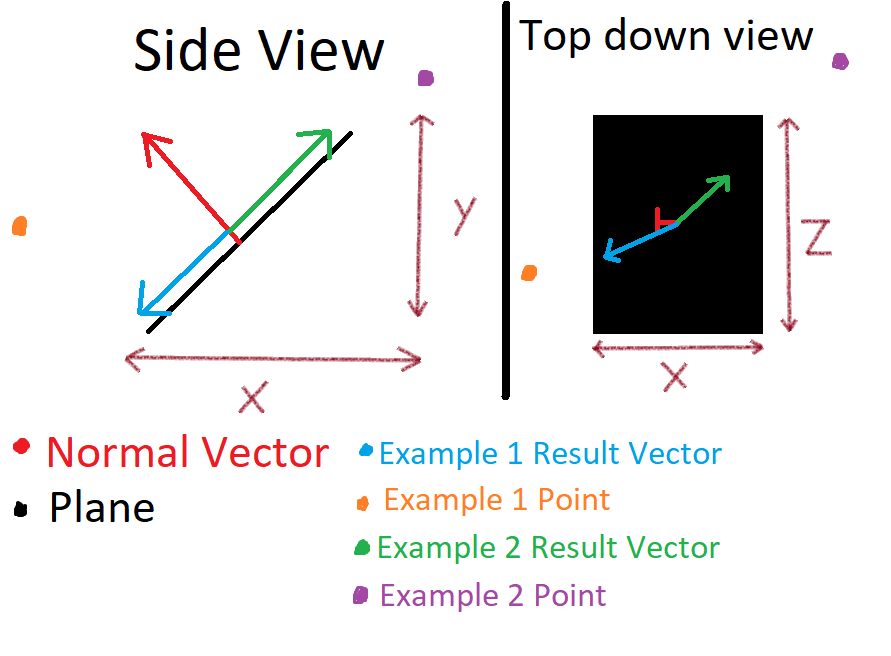
diagram

What I've tried

This is the code I've made to try to calculate the vector. It doesn't work not sure what to add to fix it.

int sgn(float val) {
    return (0.0f < val) - (val < 0.0f);
}

void DetermineVector(Vector3 normalVector, Vector3 hitPosition, Vector3 goalPoint) {
    float deltaX = goalPoint.X - hitPosition.X; // TO - FROM
    float deltaY = goalPoint.Y - hitPosition.Y; // TO - FROM
    float deltaZ = goalPoint.Z - hitPosition.Z; // TO - FROM

    // Determine the x, z components of the vector.
    // Basic Pythagorean Theorem
    float length = sqrt(deltaX * deltaX   deltaZ * deltaZ);

    float x = deltaX / length;
    float z = deltaZ / length;

    // Determine the y component of the vector;

    // Gets the sign of angle rotation
    float crossProductSum = -normalVector.X * deltaY   normalVector.Y * deltaX;
    int sign = sgn(crossProductSum); // Gets the sign -1, 0, and 1

    // Use trigonometry to figure out the angle of the normal vector in relation to the UP vector (0, 1, 0)
    // take that angle and subtract rotate 90 and take that resulting y vector and multiply the sign
    float angle = acos(normalVector.Y);
    float y = cos(angle - 90) * sign;

    // We have to combine the components so that the Y component is the same because its already normalized
    // But we have to normalize the x, z components based on the Y component
    return Vector3(x / (1 - y), y, z / (1 - y));
}

CodePudding user response：

In other words you're seeking a vector from hitPosition towards the projection of goalPoint along the Y axis. You don't need trigonometry for this.

A vector (X,Y,Z) is perpendicular to the normal of the plane if it satisfies:

X*normalVector.X   Y*normalVector.Y   Z*normalVector.Z == 0

(See dot product.)

That vector points towards the projection of goalPoint along Y axis if

X = deltaX
Z = deltaZ

Substituting and solving for Y:

Y = -(deltaX*normalVector.X   deltaZ*normalVector.Z)/normalVector.Y

You can normalize the result at the end if needed.

Putting it all together:

Vector3 DetermineVector(Vector3 normalVector, Vector3 hitPosition, Vector3 goalPoint) {
    float deltaX = goalPoint.X - hitPosition.X; // TO - FROM
    float deltaY = goalPoint.Y - hitPosition.Y; // TO - FROM
    float deltaZ = goalPoint.Z - hitPosition.Z; // TO - FROM

    float X = deltaX;
    float Y = -(deltaX*normalVector.X   deltaZ*normalVector.Z)/normalVector.Y;
    float Z = deltaZ;

    // optionally normalize:
    float length = sqrt(X*X   Y*Y   Z*Z);
    X /= length, Y /= length, Z /= length;

    return Vector3(X, Y, Z);
}