I am trying to create a Binary Search Tree (BST) for a really large txt file (around 150000 lines), but my BST is not sorting properly. My current theory is, when I fetch the key from the txt file, it doesn't register properly, making it fetch a random number from memory. Other than that, I have no idea whats wrong.
NOTE: the txt file has the following format (key on left, value on right)
0016718719 #:@-;QZL=!9v
0140100781 5:`ziuiCMMUC
0544371484 W{<_|b5Qd534
0672094320 QcvX=;[lpR("
0494074201 FB[?T5VHc7Oc
0317651971 K`9@Qn{@h]1z
0635368102 KGVm-?hX{Rv7
0107206064 =n1AsY32_.J9
0844660357 L4qL)x{>5e8H
0699014627 v/<4%"sJ4eHR
0786095462 G!cl'YMAL*@S
0067578317 6{"W,j2>@{p*
0730012647 rAi?q<X5NaKT
0715302988 ,8SrSw0rEEc&
0234601050 PRg$$:b|B0'x
0537081097 fgoDc05rc,n|
0226858124 OV##d6th'<us
1059497442 2,'n}YmK,s^i
0597822915 LhicQ#r<Yh\8
0742176394 g`XkLi.>}s Q
0984120927 DyB:-u*}E&X)
0202768627 8(&zqlPV@DCb
0089402669 tv-vTkn"AIxt
1045610730 hOxZQ<"yyew`
0671297494 )r7gD;:9FHrq
0245267004 f0oO:/Zul0<"
0766946589 n/03!]3t0Lux
0521860458 _D $,j#YT$cS
0891617938 t%gYiWV17Z/'
0566759626 r2A'PB'xhfw@
0221374897 e[-Nf"@<o9^p
0428608071 46S4!vZA.S&.
0755431241 mgE?2IewG!=g
0534588781 %P|b"_d'VF0S
0030447903 Q&Dow27tkc9
0957065636 [pHMrM*q*ED7
0739800529 wR;u\Ct/-Vzo
0556668090 =|T.z]?.:DnC
0649777919 2}5M=.u'@1,L
0464018855 x JImm6w/eG]
0460707117 lxY}\Cdn%!rs
0273053706 s9GmIAE."j|2
0596408906 %'1|R%3tI-Tz
0473143619 k,h&_7rT)?Nb
0922139211 [e0Q1].<Qb;[
0207160144 t!&lXR7`eW#n
0128147823 L,d'7]ZTvPDQ
0178779865 (&--sQ..)7d'
0531711943 4o'^xS6rK]yl
0429655621 eyd7UwKQ][%i
0566959905 k{)d*OH&w2P<
0472331841 DiZF(W"wO42H
0589473577 V0$9-X%YD_kD
0272100993 i%c&R{^#SM$@
0956804045 BtY'cQ){wR{{
0635780805 dWnP0sP2]Tu[
0874803681 swn\*HS08v<w
1027292189 w#E:LaCg(L(I
0592836099 ]&Q({r^(/H%0
0882899568 zb_4acX8E<2-
0542667063 n'xbSaoXArp6
0289624942 G5X#aqr7 *pb
0682188682 H^o)>1\4o5WV
0984355947 =Z{wmP'Z(@2r
0459720821 1vNg_4`3IUUJ
0563538441 uA>QKi]Z31#x
1032927818 $jReN<b/(e{E
0299897321 j=PAkNj#H(L^
0428967901 8lszH<!m\C`w
0668128293 SO("{Rm29l@Y
0354915591 2coM%<Iiwwn<
0672908146 r3VRE;Q3)zi>
0435139431 d_q_)mM"X]N-
0728369037 >X_!}vtc;G(M
0982520682 {h\5gbvzsqGZ
0396776915 $py=A?iNde7(
0511806860 #T Y0HI9/U6K
0013335601 <$8f|iV\=/RD
0511264736 NFI-#xssP)F*
0727884351 5ZMcmA0[K3P2
0460487630 .D'h(f"LV]@x
0178037927 o3a&fO}="I.S
Here is my Main file:
#include "LAB3BST2.h"
#include <string.h>
#define HEIGHT_WRITTEN 1
#define FINDPARENTHELPER_WRITTEN 1
#define DELETE_WRITTEN 1
#define LOOKUP_written 1
int digit(char *key) {
int number = 0;//create a
while (*key != '\0') {//loop until the end of the string (number)
number = 10 * number *key - '0';//(10*number) this represents moving the current value of key one up
//(*key - '0') the current char subtracted by '0' or the value of 48
// example: (char '1') - '0' == int 1. Reference ASCII chart to see hexadecimal logic
*key ;
}
return number;
}
int main(void) {
Node *n = NULL; // eliminates compiler warning
FILE *fp;
int c;
Tree *t = NULL;
char *pbuff = (char *)malloc(256);
char *p, *key, *pass;
int temp = 0;
long bst_node = 0;
fp = fopen("IDENTS.txt", "r");
if (!fp) {
printf("File Open Failed\n");
return 0;
}//initialize the head of the tree
while (1) {
p = fgets(pbuff, 256, fp);
if (p == NULL)
break; //memory not allocated, or end of file
while (*p == ' ')
p ; //if spaces, iterate through string
key = p;
p ;
while ((*p) >= 48 && (*p) <= 57)
p ;//if a digit character (47<p<58 or 0-9), iterate through key
*p = '\0';//null everything after the key (digits)
p ; //iterate onto the password
while (*p == ' ')
p ;//if spaces, iterate through string
pass = p;
p ;
while ((*p) != '\r' && (*p) != '\n') {
p ;
}// iterate until the end of the string ('\n')
*p = '\0';//null the rest, and reset "p"
temp = digit(key);
if (temp < 0) {
continue;
}
if (temp == 170696526) {
//nothing
}
if (t == NULL) {
t = initTree(temp, pass);
} else
insert(temp, pass, t->root);//WE NEED TO BE ABLE TO CREATE A PASS THAT DOES NOT CHANGE
bst_node ;
}
printf("\nBST NODES: %ld", bst_node);
fclose(fp);
/*
printf("Original Tree: \n");
printTree(t->root);
printf("\n\n");
if (HEIGHT_WRITTEN == 1) {
printf("Height of tree: %d\n\n", height(t->root));
}
*/
if (DELETE_WRITTEN == 1) {
FILE *fp_del;
fp_del = fopen("DELETES.txt", "r");
while (1) {
p = fgets(pbuff, 256, fp_del);
if (p == NULL)
break;
while (*p == ' ')
p ;
key = p;
p ;
while (*p != '\r' && *p != '\n') {
p ;
}
*p = '\0';
int k = withdraw(digit(key), t->root);
if (k)
bst_node--;
}
}
printf("\nNODES AFTER DELETES: %ld \n", bst_node);
if (!bst_check(t->root))
printf("NOT BST\n");
else
printf("IS A BST\n");
if (LOOKUP_written) {
FILE *fp_look;
fp_look = fopen("LOOKUPS.txt", "r");
int nnkey = 0;
while (1) {
p = fgets(pbuff, 256, fp_look);
if (p == NULL)
break;
while (*p == ' ')
p ;
key = p;
p ;
while (*p != '\r' && *p != '\n') {
p ;
}
*p = '\0';
nnkey = digit(key);
Node* k = find(nnkey, t->root);
if (!k) {
printf("ID: d PASSWORD: <NOT FOUND>\n", nnkey);
} else {
printf("ID: d PASSWORD: %s\n", nnkey, k->value);
}
}
}
return 0;
}//main()
Here is my function file
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include "LAB3BST2.h"
Node *initNode(Key k, char *v)
// Allocate memory for new node and initialize fields.
// Returns pointer to node created.
{
Node *n = malloc(sizeof(Node));
// initialize node if memory obtained
if (n != NULL) {
n->key = k;
n->value = strdup(v);
n->leftChild = NULL;
n->rightChild = NULL;
}
return n;
}//initNode()
Tree *initTree(Key k, char *v)
// Set up new tree. Allocates memory for Tree structure, then
// calls initNode() to allocate first node.
{
Tree *t = malloc(sizeof(Tree));
if (t != NULL)
t->root = initNode(k, v);
return t;
}//initTree()
void printTreeExplanation(void)
// Prints hint to reader what to expect on screen
{
static int done = 0;
if (!done) {
printf("First time explanation of tree display:\n");
printf("Every node is displayed as a comma-separated pair within brackets:");
printf(" (kk,vv)\n");
printf("where kk is the key and vv is the value\n");
printf("A tree starts with a curly bracket { and ends with a curly bracket }.\n");
printf("An empty tree will be {}\n");
printf("A tree with no children will be { (kk,vv),{},{} }\n");
printf("If either subtree is populated, it will be shown using the same ");
printf("technique as described above\n");
printf("(Hint: Start at root - and then match up all the remaining\n");
printf("brackets, then interpret what those bracket pairs are telling\n");
printf("you.)\n============\n\n");
done = 1;
}
}//printTreeExplanation()
void printTree(Node *root)
// Print whole tree. We cannot make it look pretty graphically, so we add some
// characters to make it a little easier to understand. We also don't really
// know what the value field is - it is declared to be a void pointer - so we
// treat it as though it points to an integer.
{
// assume printTree magically knows the types in the tree node
printTreeExplanation();
// start of this tree
printf("{");
// values in the root node (assuming value is pointing to an integer)
printf("(%d,%s),", root->key, root->value);
// Now show left subtree or {} if there is no left subtree
if (root->leftChild != NULL)
printTree(root->leftChild);
else
printf("{}");
// Marker between left and right subtrees
printf(",");
// Now show right subtree or {} if there is no right subtree
if (root->rightChild != NULL)
printTree(root->rightChild);
else
printf("{}");
// Close display of this tree with closing curly bracket
printf("}");
}//printTree()
Node *find(Key k, Node *root)
{
// termination conditions - either true, search is ended
if ((root == NULL) || (root->key == k))
return root;
if (k > root->key) //traverse through the right subtree (larger)
return find(k, root->rightChild);
else //traverse through the right
return find(k, root->leftChild);
}//find()
int insert(Key k, char *v, Node *root)
{
int result = BST_FAIL;
// this if statement can only be true with first root (root of whole tree)
if (root == NULL) {
Node *n = initNode(k, v);
root = n;
return BST_SUCCESS;
}
if (root->key == k)
root->value = strdup(v);//replace password
else
if (k < root->key) {
// key value less than key value in root node - try to insert into left
// subtree, if it exists.
if (root->leftChild != NULL)
// there is a left subtree - insert it
result = insert(k, v, root->leftChild);
else {
// new Node becomes the left subtree
Node *n = initNode(k, v);
root->leftChild = n;
result = BST_SUCCESS;
}
} else
if (k > root->key) { // test actually redundant
// key is greater than this nodes key value, so value goes into right
// subtree, if it exists
if (root->rightChild != NULL)
// there is a right subtree - insert new node
result = insert(k, v, root->rightChild);
else {
// no right subtree - new node becomes right subtree
Node *n = initNode(k, v);
root->rightChild = n;
result = BST_SUCCESS;
}
}
return result;
}//insert()
int intmax(int a, int b) {
return (a >= b) ? a : b;
}//intmax()
int height(Node *root)
// Height definition:
// Height of an empty tree is -1. Height of a leaf node is 0. Height of other
// nodes is 1 more than larger height of node's two subtrees.
{
int nodeheight = -1;
int right, left;// default returned for empty tree
if (root != NULL) {
left = height(root->leftChild);
right = height(root->rightChild);
nodeheight = intmax(left, right);
}
return nodeheight;
}//height()
Node *findParentHelper(Key k, Node *root)
// Help find parent of node with key == k. Parameter root is node with
// at least one child (see findParent()).
{
if (root->leftChild != NULL) {
if (root->leftChild->key == k)
return root;
}
if (root->rightChild != NULL) {
if (root->rightChild->key == k)
return root;
}
if (k > root->key)
return findParentHelper(k, root->rightChild);
else
return findParentHelper(k, root->leftChild);
}//findparenthelper()
Node *findParent(Key k, Node *root)
// root
{
// Deal with special special cases which could only happen for root
// of whole tree
if (root == NULL)
return root;
// real root doesn't have parent so we make it parent of itself
if (root->key == k)
return root;
// root has no children
if ((root->leftChild == NULL) && (root->rightChild == NULL))
return NULL;
// Deal with cases where root has at least one child
return findParentHelper(k, root);
}//findParent()
Node *findMin(Node *root) {
if (root->leftChild == NULL)
return root;
return findMin(root->leftChild);
}
Node *findMax(Node *root) {
if (root->rightChild == NULL)
return root;
return findMax(root->rightChild);
}
int check(Node *p, Node *n) {
if (p->rightChild == n)
return 1; //1==right, 0==left
return 0;
}
void delete(Node *p, Node *n)
// Delete node pointed to by n.
// Parameters:
// n - points to node to be deleted
// p - points to parent of node to be deleted.
{
// Deletion has 3 cases - no subtrees, only left or right subtree, or both
// left and right subtrees.
if (p == n) { //if the root is the node to be deleted
Node *temp;
int key;
char *pass;
if (p->rightChild) {
temp = findMin(p->rightChild);
key = temp->key;
pass = strdup(temp->value);
delete(findParent(temp->key, n), temp);
p->key = key;
p->value = pass;
} else
if (p->leftChild) {
temp = findMax(p->leftChild);
key = temp->key;
pass = strdup(temp->value);
delete(findParent(temp->key, n), temp);
p->key = key;
p->value = pass;
}
return;
}
if (n->leftChild != NULL) { // there is left child
if (n->rightChild) { //if both
Node *temp = findMin(n->rightChild);
n->key = temp->key;
n->value = strdup(temp->value);
delete(findParent(temp->key, n), temp);//delete the min value found (which is a leaf on the left most right branch)
} else { //if only left
if (check(p, n)) {
p->rightChild = n->leftChild;
} else
p->leftChild = n->leftChild;
free(n);
}
} else
if (n->rightChild) { // there is only a right child
if (check(p, n)) {
p->rightChild = n->rightChild;
} else
p->leftChild = n->rightChild;
free(n);
} else {// no children
if (check(p, n)) {
p->rightChild = NULL;
} else
p->leftChild = NULL;
free(n);
}
}//delete()
int withdraw(Key k, Node *root)
// Withdraw does two things:
// return a copy of the node with key k (and value v)
// Delete the node with key k from the tree while ensuring the tree remains valid
{
Node *p, *m;
m = find(k, root);
if (m != NULL) {
// create a copy of the node with the same key and value
//n = initNode(m->key, m->value);
p = findParent(k, root);
// can delete the node
delete(p, m);
return 1;
}
return 0;
}//withdraw()
int bst_check(Node *root) {
if (root == NULL)
return 1; // if on a leaf (return back up to root) //170696526
if (root->leftChild != NULL && root->leftChild->key > root->key)
//if the left child exists and its key is greater than the root
return 0;
if (root->rightChild != NULL && root->rightChild->key < root->key)
// if the right child exists and is smaller than the root
return 0;
if (!bst_check(root->leftChild) || !bst_check(root->rightChild))
//if the check was unsuccessful for both the right and left subtrees
//also recursively checks the left and right child
return 0;
//if all pass, then the tree was a bst
return 1;
}
Here is my function file (.h file):
// LAB3_BST.H
// Header file to be used with code for ELEC278 Lab 3.
//
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
typedef int Key;
#define BST_FAIL 0 // return value when BST function fails
#define BST_SUCCESS 1 // return value when BST function succeeds
// Node in tree has key and pointer to value associated with key.
// Also contains structural components - two pointers to left and
// right subtrees.
typedef struct password {
char *word;
struct password *next;
} pnode;
typedef struct Node {
Key key;
char *value;
struct Node *leftChild, *rightChild;
} Node, pNode;
// Tree is basically pointer to top node in a tree.
typedef struct Tree {
Node *root;
} Tree;
Node *initNode(int k, char *v);
// Create new tree by creating new node with key = k and value = v
// and making it root
Tree *initTree(int k, char *v);
// Find node with key k in tree. Returns pointer to Node if found;
// Returns NULL if not found
Node *find(Key k, Node *root);
// Create new node with key=k, value=v and insert it into tree
// Returns 1 upon success, 0 failure
int insert(int k, char *v, Node *root);
// Print text representation of tree (starting at any Node)
void printTree(Node *root);
// Returns Maximum of two integer numbers
int intmax(int a, int b);
// Find parent of node n where n->key = k
// Returns pointer to parent node if found; Returns NULL if not found
Node *findParent(Key k, Node *root);
// 1. Make copy of node with key=k and returns it
// 2. Delete node with key=k from tree
// Return pointer of node created in 1; Returns NULL if no node
// with specified key value is found
int withdraw(Key k, Node *root);
// Return height of tree (height of specified root)
int height(Node *root);
// Helper function for findParent - see specification in lab
// instructions
Node *findParentHelper(Key k, Node *root);
// Delete node from tree while ensuring tree remains valid
void delete(Node *p, Node *n);
Node* inorder(Node *pn);
int bst_check(Node *root);
I dont know where to start.
CodePudding user response:
There are some problems in function insert:
- if the
rootargument is NULL, the new node is just stored into the argument pointer andBST_SUCCESSis returned. The caller's node variable is not updated. This function should take the address of theNode*as an argument. In your case, the tree is initialized as non empty, so this never occurs, but the tree will become empty after removing all elements and in this case,insertwill always fail in spite of returningBST_SUCCESS. - if
root->key == k, a new value is allocated for this duplicate key, but the previous value is not freed, hence there is a memory leak. - the test
else if (k > root->key)is indeed redundant
Here is a modified and much simpler version:
int insert(Key k, const char *v, Node **np) {
Node *node = *np;
if (node == NULL) {
*np = initNode(k, v);
if (*np == NULL)
return BST_FAIL;
else
return BST_SUCCESS;
}
if (k == node->key) {
// node exists, replace password
char *str = strdup(v);
if (str == NULL) {
return BST_FAIL;
} else {
free(node->value);
node->value = str;
return BST_SUCCESS; // no new node, but insertion successful
}
}
if (k < node->key) {
// key value is less than key value in this node
// insert it into left subtree, creating it if needed.
return insert(k, v, &node->leftChild);
} else {
// key value is greater than key value in this node
// insert it into right subtree, creating it if needed.
return insert(k, v, &node->rightChild);
}
}
Here is a non recursive version:
int insert(Key k, const char *v, Node **np) {
while (*np) {
Node *node = *np;
if (k == node->key) {
// node exists, replace password
char *str = strdup(v);
if (str == NULL) {
return BST_FAIL;
} else {
free(node->value);
node->value = str;
return BST_SUCCESS; // no new node, but insertion successful
}
}
if (k < node->key) {
// key value is less than key value in this node
// insert it into left subtree, creating it if needed.
np = &root->leftChild;
} else {
// key value is greater than key value in this node
// insert it into right subtree, creating it if needed.
np = &root->rightChild;
}
}
*np = initNode(k, v);
if (*np == NULL)
return BST_FAIL;
else
return BST_SUCCESS;
}
Note however that neither of the above functions implement a balanced tree (BST). The tree needs rebalancing if the height of left and right child nodes' heights become too different.
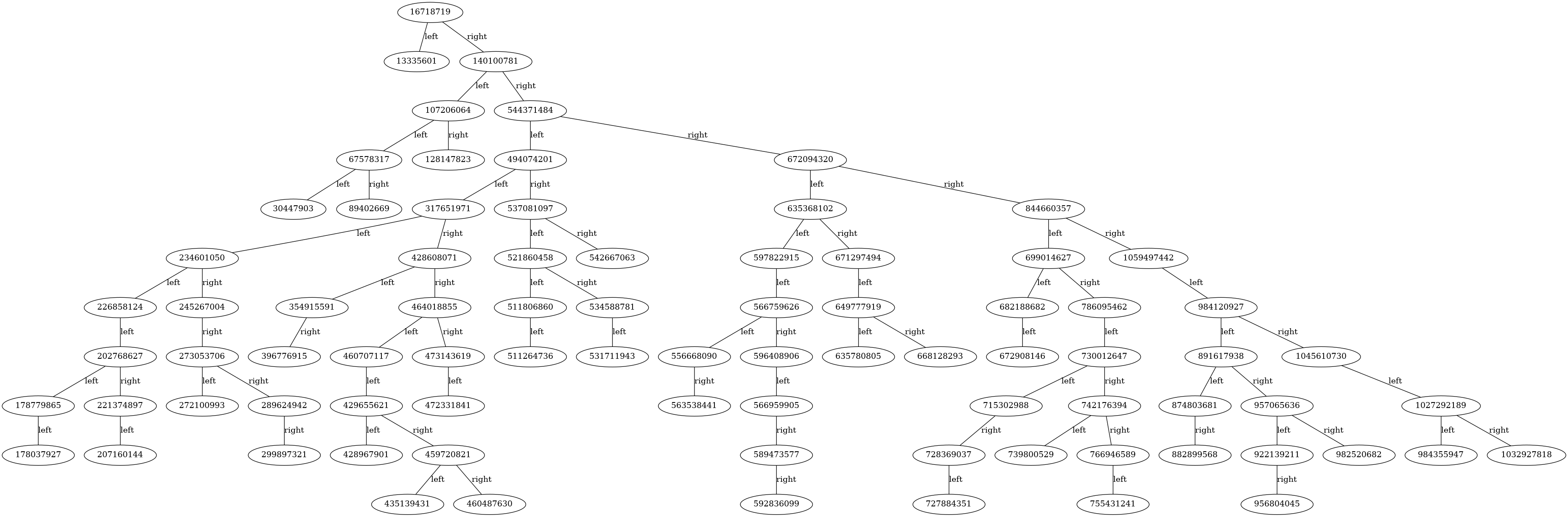
CodePudding user response:
This is not an answer but wanted to add a graph of the input data. I don't see anything out of order (i.e. non-reproducable):