How do I create a 2d color gradient plot using matplotlib?-CodePudding

I am trying to create a 2D plot where the 4 quadrants represent four distinct phases. As an example, I want it to look something like this:

Except that I want the center and all the lines of intersection to have more white in them.

In an attempt to this, I created a color mixer:

def combine_hex_values(d):
    d_items = sorted(d.items())
    tot_weight = sum(d.values())
    red = int(sum([int(k[:2], 16)*v for k, v in d_items])/tot_weight)
    green = int(sum([int(k[2:4], 16)*v for k, v in d_items])/tot_weight)
    blue = int(sum([int(k[4:6], 16)*v for k, v in d_items])/tot_weight)
    zpad = lambda x: x if len(x)==2 else '0'   x
    return zpad(hex(red)[2:])   zpad(hex(green)[2:])   zpad(hex(blue)[2:])

which takes in a color dictionary with hex values and creates mixed colors if you change the proportion of the contents. For example,

# green, red, blue, yellow, white
cdict = {"00FF00": 0, "FF0000": 0, "0000FF": 1, "FFFF00": 0, "FFFFFF": 0}
c = "#" combine_hex_values (cdict) 

keyg = "00FF00"; keyr = "FF0000"; keyb = "0000FF"; keyy = "FFFF00"; keyw = "FFFFFF";

will create the hex value c for blue. However, I don't know how to go about assigning each lattice point a color. This is not a contour, as every point gets a unique color. This is my trivial attempt:

xpoints = np.linspace (-1, 1, 10)
ypoints = np.linspace (-1, 1, 10)

R = np.sqrt(2) 

color_list = []

xlat = []
ylat = [] 

for x in xpoints:
    for y in ypoints:
        for key in cdict:
            cdict[key] = 0
        r = np.sqrt(x*x   y*y) 
        cdict[keyw] = 1 - r/R 
        
        if x > 0 and y > 0: 
            cdict[keyb] = r/R
        elif x > 0 and y < 0:
            cdict[keyy] = r/R
        elif x < 0 and y > 0:
            cdict[keyr] = r/R
        elif x < 0 and y < 0:
            cdict[keyg] = r/R 

        color_list.append ( "#" combine_hex_values (cdict) )
        xlat.append (x)
        ylat.append (y)

plt.scatter (xlat, ylat, c=color_list, s=90)
plt.show()

This creates a plot, but it is very discrete at the edges, and it is still markers which do not fill up the entire surface.

How can I go about making the image I have above (do not need the grid lines)?

CodePudding user response：

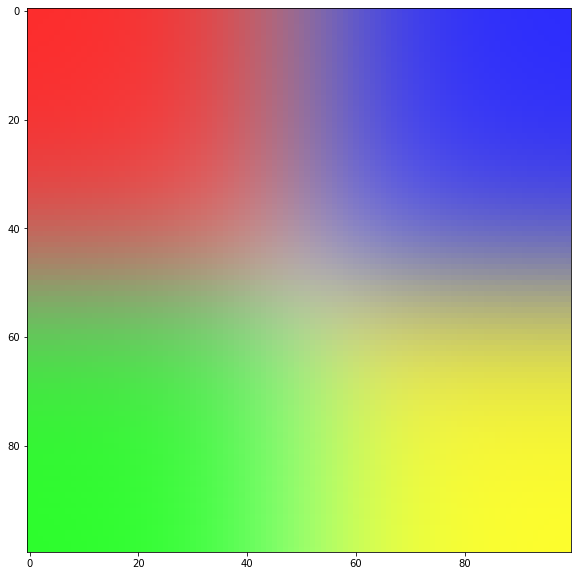
After playing around with a few approaches, these are the nicest results I got using imshow.

If you want to use this as an intermediate step towards another method, note that result[i][j] is an array [R,G,B], with each somewhere from 0 to 1.

n = 100        # resolution along each side
lighten = .3   # factor by which to lighten corner colors
sigma = .07    # higher sigma -> more blending

# colors proceed clockwise from upper-right corner
colors = [[1,0,0],  # red
          [0,0,1],  # blue
          [1,1,0],  # yellow
          [0,1,0],] # green
colors = np.array(colors)
colors = lighten   (1-lighten)*colors

# create 2D gradient emanating from top-left
half_range = np.linspace(0,.5,n)
grad = np.exp(-((half_range**2   half_range[:,None]**2)/sigma))
grad = grad - grad[-1,-1]
grad/=np.max(grad)
grad[grad<0] = 0

# get color contributions to each point of each corner
grads = []
layers = []
for c in colors:
    layers.append(grad[:,:,None]*c[None,None,:]) # color contribution of c-colored corner
    grads.append(grad)
    grad = grad.T[:,::-1] # rotate gradient
layers = np.array(layers)
tot = np.array(grads).sum(axis = 0)

# combine colors at each point
p = 2
result = np.average(layers**p,axis = 0)**(1/p)/tot[:,:,None]

# saturate colors
result /= np.max(result)

plt.imshow(result)

Resulting image:

An alternative, taking a "subtractive" approach then saturating in post.

n = 100         # resolution along each side
# lighten = 0   # factor by which to lighten corner colors
darken = 0
sigma = .05     # higher sigma -> more blending
sat = 0.4       # amount by which to "saturate" the final image (above .5 leads to data clipping)

# colors proceed clockwise from upper-right corner
colors = [[1,0,0],  # red
          [0,0,1],  # blue
          [1,1,0],  # yellow
          [0,1,0],] # green
colors = np.array(colors)
colors = (1-darken)*colors
colors = 1-colors

# create 2D gradient emanating from top-left
half_range = np.linspace(0,.5,n)
grad = np.exp(-((half_range**2   half_range[:,None]**2)/sigma))
grad = grad - grad[-1,-1]
grad/=np.max(grad)
grad[grad<0] = 0

# get color contributions to each point of each corner
grads = []
layers = []
for c in colors:
    layers.append(grad[:,:,None]*c[None,None,:]) # color contribution of c-colored corner
    grads.append(grad)
    grad = grad.T[:,::-1] # rotate gradient
layers = np.array(layers)
tot = np.array(grads).sum(axis = 0)

# combine colors at each point
p = 2
result = 1-np.average(layers**p,axis = 0)**(1/p)/tot[:,:,None]

# saturate colors
result = (result - sat)/(1 - sat)

plt.imshow(result)

Result: