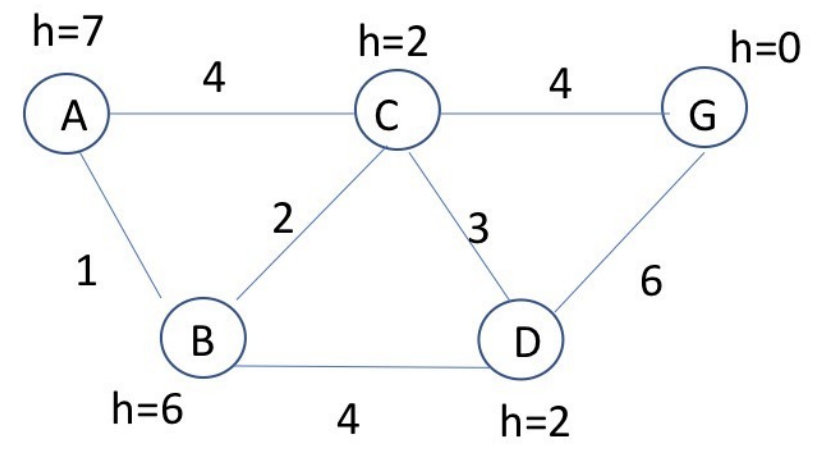
I am wondering why the order of expansion is ACBDG and not just ACG. From what i understand from the A*-algorithm is that is uses the f-value, which is the heuristic value and the real cost combined to determine the next node to expand. Is is that when expanding a node, the previous cost will be the f-value from the next node and current node combined? Or the f-value of the next node and g-value from current node combined?
It seems strange that after expanding the A, C and B nodes that the next node would not be G, as H(G) is lower than H(D). I observe that the real cost is lower to D, but isnt the point of A* to go for the combined heuristic value and the actual cost?
The starting node is A and the goal is G
CodePudding user response:
In the following steps to the left of the => are the unexpanded nodes, and on the right are the action and the result of the expansion. Nodes on the left contain between the parenthesis the path, the cost of that path, and heuristic value. On the right there is no heuristic value yet. Nodes on the left are sorted by cost of path heuristic value, with later nodes added after the existing nodes if they have equal sums:
- A(-, 7) => Expand A from -: got B(A, 1), C(A, 4)
- C(A, 4, 2), B(A, 1, 6) => Expand C from A: got B(AC, 6), D(AC, 7), G(AC, 8)
- B(A, 1, 6), G(AC, 8, 0), D(AC, 7, 2), B(AC, 6, 6) => Expand B from A: got C(AB, 3), D(AB, 5)
- C(AB, 3, 2), D(AB, 5, 2), G(AC, 8, 0), D(AC, 7, 2), B(AC, 6, 6) => Expand C from AB: got D(ABC, 6), G(ABC, 7)
- D(AB, 5, 2), G(ABC, 7, 0), G(AC, 8, 0), D(ABC, 6, 2), D(AC, 7, 2), B(AC, 6, 6) => Expand D from AB: got C(ABD, 8), G(ABD, 11)
- G(ABC, 7, 0), G(AC, 8, 0), D(ABC, 6, 2), D(AC, 7, 2), C(ABD, 8, 2), G(ABD, 11, 0), B(AC, 6, 6) => Found G from ABC, end of search